• 361 can be written using four 4's:
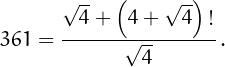
361 has 3 divisors (see below), whose sum is σ = 381. Its totient is φ = 342.
The previous prime is 359. The next prime is 367. The reversal of 361 is 163.
The square root of 361 is 19.
It is a perfect power (a square), and thus also a powerful number.
361 is nontrivially palindromic in base 15.
It is a semiprime because it is the product of two primes, and also a brilliant number, because the two primes have the same length.
It is not a de Polignac number, because 361 - 21 = 359 is a prime.
It is a hoax number, since the sum of its digits (10) coincides with the sum of the digits of its distinct prime factors.
It is an alternating number because its digits alternate between odd and even.
It is a Duffinian number.
361 is an undulating number in base 15.
361 is a lucky number.
It is a plaindrome in base 14 and base 16.
It is a nialpdrome in base 8 and base 9.
It is a panconsummate number.
It is not an unprimeable number, because it can be changed into a prime (367) by changing a digit.
It is a pernicious number, because its binary representation contains a prime number (5) of ones.
It is a polite number, since it can be written in 2 ways as a sum of consecutive naturals, for example, 10 + ... + 28.
It is an arithmetic number, because the mean of its divisors is an integer number (127).
2361 is an apocalyptic number.
361 is the 19-th square number.
361 is the 16-th centered triangular number, the 10-th centered octagonal number and also the 9-th centered decagonal number.
It is an amenable number.
361 is a deficient number, since it is larger than the sum of its proper divisors (20).
361 is an equidigital number, since it uses as much as digits as its factorization.
361 is an odious number, because the sum of its binary digits is odd.
The sum of its prime factors is 38 (or 19 counting only the distinct ones).
The product of its digits is 18, while the sum is 10.
The cubic root of 361 is about 7.1203673589.
Subtracting from 361 its sum of digits (10), we obtain a triangular number (351 = T26).
Subtracting from 361 its product of digits (18), we obtain a palindrome (343).
It can be divided in two parts, 3 and 61, that added together give a 6-th power (64 = 26).
The spelling of 361 in words is "three hundred sixty-one", and thus it is an aban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.070 sec. • engine limits •

