The generalized Woodall numbers up to 1015 :
1, 7, 17, 23, 63, 80, 159, 191, 323, 383, 895, 1023, 1214, 2047, 2499, 4373, 4607, 5119, 10239, 15308, 15624, 22527, 24575, 38879, 49151, 52487, 93749, 106495, 114687, 177146, 229375, 279935, 491519, 524287, 546874, 590489, 705893, 1048575, 1948616, 1959551, 2228223, 2359295, 3124999, 4718591, 5764800, 6377291, 9961471, 10485759, 13436927, 14680063, 17578124, 20726198, 20971519, 44040191, 46118407, 46137343, 66961565, 90699263, 92274687, 97656249, 134217727, 192937983, 201326591, 215233604, 344373767, 363182462, 402653183, 537109374, 604661759, 688747535, 838860799, 872415231, 1207959551, 1744830463, 2195382770, 2824752489, 2929687499, 3486784400, 3623878655, 3758096383, 3990767615, 6973568801, 7516192767, 8999999999, 10737418239, 15569256447, 15869140624, 16106127359, 21750594172, 22082967872, 26121388031, 32212254719, 34867844009, 66571993087, 68719476735, 69735688019, 85449218749, 94489280511, 99999999999, 137438953471, 166095446411, 169789022207, 219667417262, 259374246009, 283467841535, 292057776127, 345191655698, 457763671874, 584115552255, 690383311397, 824633720831, 1097098297343, 1099999999999, 1202590842879, 1236950581247, 1259557135290, 2165293113020, 2441406249999, 2473901162495, 3138428376720, 3389154437771, 5085241278463, 5222680231935, 6778308875543, 7052774768639, 7146825580543, 8173092077567, 9495123019885, 10445360463871, 11999999999999, 12969970703124, 21182215236074, 21440476741631, 21990232555519, 33044255768276, 37661140520651, 43980465111039, 45137758519295, 61572651155455, 66088511536553, 68664550781249, 71213422649144, 90159953477631, 92358976733183, 106993205379071, 129999999999999, 184717953466367, 205891132094648, 279577021469771, 287753210560511, 320275094369453, 362396240234374, 378231999954943, 387028092977151, 448795257871102, 527765581332479, 531726889113615, 640550188738907, 774056185954303.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 159 values, from 1 to 9.99⋅1030107).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 0 | 100000 | 2 | ||||||||
| 3 | 33333 | 33334 | 33333 | 3 | |||||||
| 4 | 0 | 1 | 0 | 99999 | 4 | ||||||
| 5 | 20000 | 20000 | 20000 | 20000 | 20000 | 5 | |||||
| 6 | 0 | 33334 | 0 | 33333 | 0 | 33333 | 6 | ||||
| 7 | 14286 | 14286 | 14285 | 14286 | 14286 | 14286 | 14285 | 7 | |||
| 8 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 99999 | 8 | ||
| 9 | 11111 | 11111 | 11110 | 11110 | 11112 | 11112 | 11112 | 11111 | 11111 | 9 | |
| 10 | 0 | 20000 | 0 | 20000 | 0 | 20000 | 0 | 20000 | 0 | 20000 | 10 |
| 11 | 9090 | 9093 | 9090 | 9090 | 9091 | 9091 | 9090 | 9091 | 9091 | 9093 | 9090 |
A pictorial representation of the table above
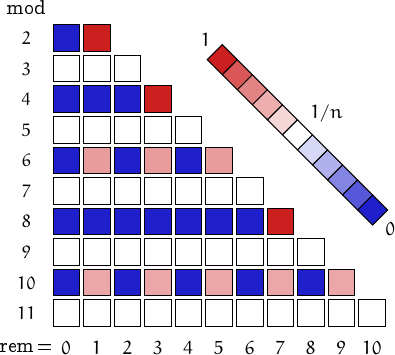
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits