The first 600 odious numbers :
1, 2, 4, 7, 8, 11, 13, 14, 16, 19, 21, 22, 25, 26, 28, 31, 32, 35, 37, 38, 41, 42, 44, 47, 49, 50, 52, 55, 56, 59, 61, 62, 64, 67, 69, 70, 73, 74, 76, 79, 81, 82, 84, 87, 88, 91, 93, 94, 97, 98, 100, 103, 104, 107, 109, 110, 112, 115, 117, 118, 121, 122, 124, 127, 128, 131, 133, 134, 137, 138, 140, 143, 145, 146, 148, 151, 152, 155, 157, 158, 161, 162, 164, 167, 168, 171, 173, 174, 176, 179, 181, 182, 185, 186, 188, 191, 193, 194, 196, 199, 200, 203, 205, 206, 208, 211, 213, 214, 217, 218, 220, 223, 224, 227, 229, 230, 233, 234, 236, 239, 241, 242, 244, 247, 248, 251, 253, 254, 256, 259, 261, 262, 265, 266, 268, 271, 273, 274, 276, 279, 280, 283, 285, 286, 289, 290, 292, 295, 296, 299, 301, 302, 304, 307, 309, 310, 313, 314, 316, 319, 321, 322, 324, 327, 328, 331, 333, 334, 336, 339, 341, 342, 345, 346, 348, 351, 352, 355, 357, 358, 361, 362, 364, 367, 369, 370, 372, 375, 376, 379, 381, 382, 385, 386, 388, 391, 392, 395, 397, 398, 400, 403, 405, 406, 409, 410, 412, 415, 416, 419, 421, 422, 425, 426, 428, 431, 433, 434, 436, 439, 440, 443, 445, 446, 448, 451, 453, 454, 457, 458, 460, 463, 465, 466, 468, 471, 472, 475, 477, 478, 481, 482, 484, 487, 488, 491, 493, 494, 496, 499, 501, 502, 505, 506, 508, 511, 512, 515, 517, 518, 521, 522, 524, 527, 529, 530, 532, 535, 536, 539, 541, 542, 545, 546, 548, 551, 552, 555, 557, 558, 560, 563, 565, 566, 569, 570, 572, 575, 577, 578, 580, 583, 584, 587, 589, 590, 592, 595, 597, 598, 601, 602, 604, 607, 608, 611, 613, 614, 617, 618, 620, 623, 625, 626, 628, 631, 632, 635, 637, 638, 641, 642, 644, 647, 648, 651, 653, 654, 656, 659, 661, 662, 665, 666, 668, 671, 672, 675, 677, 678, 681, 682, 684, 687, 689, 690, 692, 695, 696, 699, 701, 702, 704, 707, 709, 710, 713, 714, 716, 719, 721, 722, 724, 727, 728, 731, 733, 734, 737, 738, 740, 743, 744, 747, 749, 750, 752, 755, 757, 758, 761, 762, 764, 767, 769, 770, 772, 775, 776, 779, 781, 782, 784, 787, 789, 790, 793, 794, 796, 799, 800, 803, 805, 806, 809, 810, 812, 815, 817, 818, 820, 823, 824, 827, 829, 830, 832, 835, 837, 838, 841, 842, 844, 847, 849, 850, 852, 855, 856, 859, 861, 862, 865, 866, 868, 871, 872, 875, 877, 878, 880, 883, 885, 886, 889, 890, 892, 895, 896, 899, 901, 902, 905, 906, 908, 911, 913, 914, 916, 919, 920, 923, 925, 926, 929, 930, 932, 935, 936, 939, 941, 942, 944, 947, 949, 950, 953, 954, 956, 959, 961, 962, 964, 967, 968, 971, 973, 974, 976, 979, 981, 982, 985, 986, 988, 991, 992, 995, 997, 998, 1001, 1002, 1004, 1007, 1009, 1010, 1012, 1015, 1016, 1019, 1021, 1022, 1024, 1027, 1029, 1030, 1033, 1034, 1036, 1039, 1041, 1042, 1044, 1047, 1048, 1051, 1053, 1054, 1057, 1058, 1060, 1063, 1064, 1067, 1069, 1070, 1072, 1075, 1077, 1078, 1081, 1082, 1084, 1087, 1089, 1090, 1092, 1095, 1096, 1099, 1101, 1102, 1104, 1107, 1109, 1110, 1113, 1114, 1116, 1119, 1120, 1123, 1125, 1126, 1129, 1130, 1132, 1135, 1137, 1138, 1140, 1143, 1144, 1147, 1149, 1150, 1153, 1154, 1156, 1159, 1160, 1163, 1165, 1166, 1168, 1171, 1173, 1174, 1177, 1178, 1180, 1183, 1184, 1187, 1189, 1190, 1193, 1194, 1196, 1199.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 5000001 values, from 1 to 10000001).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 2500000 | 2500001 | 2 | ||||||||
| 3 | 1557344 | 1754997 | 1687660 | 3 | |||||||
| 4 | 1250000 | 1250001 | 1250000 | 1250000 | 4 | ||||||
| 5 | 996565 | 1000286 | 1002630 | 1000000 | 1000520 | 5 | |||||
| 6 | 767449 | 899218 | 876772 | 789895 | 855779 | 810888 | 6 | ||||
| 7 | 713579 | 714300 | 714321 | 714800 | 713723 | 714443 | 714835 | 7 | |||
| 8 | 625000 | 625001 | 625000 | 625000 | 625000 | 625000 | 625000 | 625000 | 8 | ||
| 9 | 519096 | 584996 | 562546 | 519139 | 585008 | 562542 | 519109 | 584993 | 562572 | 9 | |
| 10 | 498090 | 501911 | 501005 | 498995 | 501525 | 498475 | 498375 | 501625 | 501005 | 498995 | 10 |
| 11 | 454479 | 454603 | 454624 | 454498 | 454578 | 454480 | 454469 | 454612 | 454613 | 454517 | 454528 |
A pictorial representation of the table above
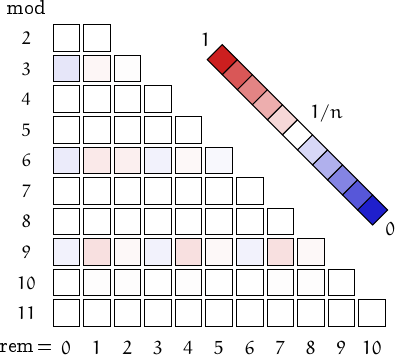
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits