The 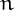 -th Bell number
-th Bell number 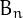 is equal to the number of ways in which
is equal to the number of ways in which
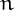 objects can be partitioned into non-empty subsets.
objects can be partitioned into non-empty subsets.
![\[
B_{n+1}=\sum_{k=0}^n{n\choose k}B_k\,,\quad\quad%
B_n = \left\lceil\frac{1}{e}\sum_{k=1}^{2n}\frac{k^n}{k!}\right\rceil\,.\]](pic.10.png)
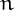 -th Bell number
-th Bell number 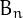 is equal to the number of ways in which
is equal to the number of ways in which
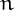 objects can be partitioned into non-empty subsets.
objects can be partitioned into non-empty subsets.
For example, 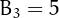 because the set
because the set 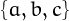 can be partitioned in
5 ways:
can be partitioned in
5 ways: 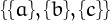 ,
, 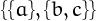 ,
, 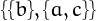 ,
, 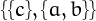 and
and 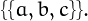
Two classical formulas
![\[
B_{n+1}=\sum_{k=0}^n{n\choose k}B_k\,,\quad\quad%
B_n = \left\lceil\frac{1}{e}\sum_{k=1}^{2n}\frac{k^n}{k!}\right\rceil\,.\]](pic.10.png)
The first Bell numbers are 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, 678570, 4213597, 27644437, 190899322, 1382958545, 10480142147, 82864869804, 682076806159, 5832742205057, 51724158235372, 474869816156751.
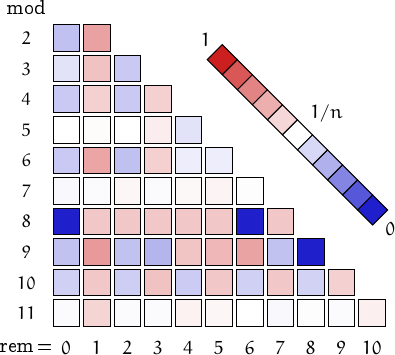
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

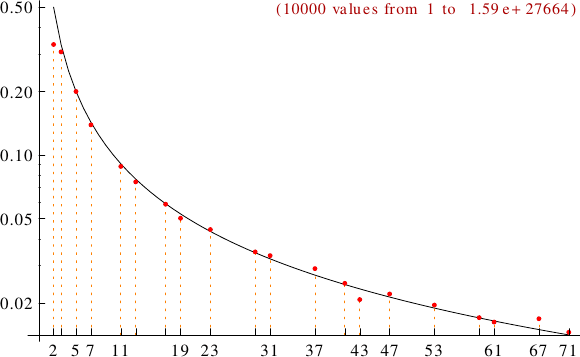
A graph displaying how many Bell numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Bell numbers can also be... (you may click on names or numbers)
aban
15
52
203
877
abundant
4140
678570
alternating
52
amenable
52
877
4140
4213597
27644437
apocalyptic
4140
21147
arithmetic
15
203
877
4140
21147
678570
4213597
astonishing
15
binomial
15
brilliant
15
cake
15
Chen
877
congruent
15
52
877
115975
4213597
constructible
15
Cunningham
15
cyclic
15
877
4213597
D-number
15
de Polignac
877
decagonal
52
deficient
15
52
203
877
21147
115975
4213597
dig.balanced
15
52
678570
190899322
double fact.
15
Duffinian
203
4213597
eban
52
economical
15
203
877
115975
emirpimes
15
203
equidigital
15
203
877
115975
evil
15
4140
21147
115975
678570
4213597
27644437
190899322
gapful
4213597
happy
203
Harshad
4140
hexagonal
15
iban
203
4140
21147
idoneal
15
inconsummate
21147
interprime
15
678570
junction
27644437
katadrome
52
Lehmer
15
lucky
15
21147
Lynch-Bell
15
magic
15
magnanimous
52
203
metadrome
15
modest
203
nialpdrome
52
877
nude
15
oban
15
877
odious
52
203
877
panconsummate
15
pandigital
15
partition
15
pernicious
52
203
877
plaindrome
15
practical
4140
prime
877
27644437
pseudoperfect
4140
678570
repunit
15
Ruth-Aaron
15
semiprime
15
203
sliding
52
sphenic
4213597
strong prime
877
tau
4140
tetranacci
15
triangular
15
uban
15
52
unprimeable
4140
untouchable
52
wasteful
52
4140
21147
678570
4213597
weak prime
27644437
Zuckerman
15
Zumkeller
4140