Search a number
Jacobsthal numbers

Search a number

(max 15 digits)

Members of the sequence defined by the recurrence J(0)=0, J(1)=1 and J(n-1) = J(n-1) + 2⋅J(n-2). more

The Jacobsthal numbers up to 1015 :
1, 3, 5, 11, 21, 43, 85, 171, 341, 683, 1365, 2731, 5461, 10923, 21845, 43691, 87381, 174763, 349525, 699051, 1398101, 2796203, 5592405, 11184811, 22369621, 44739243, 89478485, 178956971, 357913941, 715827883, 1431655765, 2863311531, 5726623061, 11453246123, 22906492245, 45812984491, 91625968981, 183251937963, 366503875925, 733007751851, 1466015503701, 2932031007403, 5864062014805, 11728124029611, 23456248059221, 46912496118443, 93824992236885, 187649984473771, 375299968947541, 750599937895083.

Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 10000 values, from 1 to 1.33⋅103010).

n\r 0  1 
2010000 2 
3333333333334 3 
40500005000 4 
525005000025000 5 
6033330333303334 6 
71666333301667166716670 7 
801050000499900 8 
9111111111111111211111111111011111112 9 
100500002500025000000 10 
1120002000010000100010000100002000

A pictorial representation of the table above
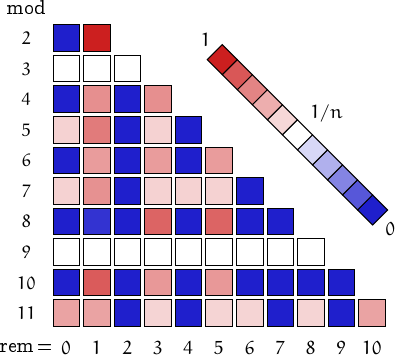
motab
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.