The first 600 Ormiston numbers :
1913, 1931, 18379, 18397, 19013, 19031, 25013, 25031, 34613, 34631, 35617, 35671, 35879, 35897, 36979, 36997, 37379, 37397, 37813, 37831, 40013, 40031, 40213, 40231, 40639, 40693, 45613, 45631, 48091, 48109, 49279, 49297, 51613, 51631, 55313, 55331, 56179, 56197, 56713, 56731, 58613, 58631, 63079, 63097, 63179, 63197, 64091, 64109, 65479, 65497, 66413, 66431, 74779, 74797, 75913, 75931, 76213, 76231, 76579, 76597, 76679, 76697, 85313, 85331, 88379, 88397, 90379, 90397, 90679, 90697, 93113, 93131, 94379, 94397, 96079, 96097, 97213, 97231, 98737, 98773, 109279, 109297, 112979, 112997, 114013, 114031, 115613, 115631, 116113, 116131, 116293, 116329, 122579, 122597, 123379, 123397, 124213, 124231, 126079, 126097, 126613, 126631, 127979, 127997, 128413, 128431, 131413, 131431, 131713, 131731, 133813, 133831, 135479, 135497, 139091, 139109, 139813, 139831, 140779, 140797, 144013, 144031, 145091, 145109, 145879, 145897, 147179, 147197, 151579, 151597, 152879, 152897, 159079, 159097, 162091, 162109, 163679, 163697, 164513, 164531, 171679, 171697, 174413, 174431, 178513, 178531, 182279, 182297, 184013, 184031, 187237, 187273, 187513, 187531, 190979, 190997, 193013, 193031, 194179, 194197, 194413, 194431, 201979, 201997, 211979, 211997, 215279, 215297, 216379, 216397, 222713, 222731, 224813, 224831, 227113, 227131, 228713, 228731, 231613, 231631, 235979, 235997, 239713, 239731, 240113, 240131, 240437, 240473, 244091, 244109, 246713, 246731, 249779, 249797, 250091, 250109, 254179, 254197, 256813, 256831, 260213, 260231, 269579, 269597, 271079, 271097, 271879, 271897, 273979, 273997, 276781, 276817, 277279, 277297, 277513, 277531, 277579, 277597, 280013, 280031, 280979, 280997, 286813, 286831, 287579, 287597, 290879, 290897, 293413, 293431, 301813, 301831, 304813, 304831, 309713, 309731, 310379, 310397, 312313, 312331, 321091, 321109, 326479, 326497, 327779, 327797, 336613, 336631, 338213, 338231, 343337, 343373, 345413, 345431, 345979, 345997, 349313, 349331, 351079, 351097, 351479, 351497, 351779, 351797, 355679, 355697, 357179, 357197, 357437, 357473, 359783, 359837, 363379, 363397, 365213, 365231, 366479, 366497, 369079, 369097, 371779, 371797, 379513, 379531, 379579, 379597, 386279, 386297, 392113, 392131, 393779, 393797, 394879, 394897, 399079, 399097, 400579, 400597, 402613, 402631, 403079, 403097, 408979, 408997, 411013, 411031, 414413, 414431, 415013, 415031, 415213, 415231, 416513, 416531, 421313, 421331, 424313, 424331, 432613, 432631, 439613, 439631, 447137, 447173, 451313, 451331, 451879, 451897, 454313, 454331, 454637, 454673, 455579, 455597, 456293, 456329, 462079, 462097, 462113, 462131, 464879, 464897, 465337, 465373, 469379, 469397, 470279, 470297, 473479, 473497, 473579, 473597, 478679, 478697, 478879, 478897, 480713, 480731, 481513, 481531, 485479, 485497, 487979, 487997, 489613, 489631, 491279, 491297, 497813, 497831, 500179, 500197, 502339, 502393, 502613, 502631, 505213, 505231, 508037, 508073, 512779, 512797, 518813, 518831, 522479, 522497, 526913, 526931, 530713, 530731, 535679, 535697, 536513, 536531, 541613, 541631, 542837, 542873, 543113, 543131, 545213, 545231, 546179, 546197, 550813, 550831, 551179, 551197, 552379, 552397, 552917, 552971, 558091, 558109, 558179, 558197, 558913, 558931, 558979, 558997, 559813, 559831, 562813, 562831, 565937, 565973, 565979, 565997, 567013, 567031, 569479, 569497, 570113, 570131, 573179, 573197, 577879, 577897, 579179, 579197, 580417, 580471, 584879, 584897, 586237, 586273, 594379, 594397, 594679, 594697, 599213, 599231, 601379, 601397, 602179, 602197, 602279, 602297, 604013, 604031, 604379, 604397, 611113, 611131, 619313, 619331, 621679, 621697, 622313, 622331, 623071, 623107, 625213, 625231, 625979, 625997, 634013, 634031, 637079, 637097, 646379, 646397, 648079, 648097, 649879, 649897, 654679, 654697, 657413, 657431, 661679, 661697, 666091, 666109, 668417, 668471, 670279, 670297, 672079, 672097, 675113, 675131, 679279, 679297, 681913, 681931, 682679, 682697, 684091, 684109, 685679, 685697, 687413, 687431, 688679, 688697, 689113, 689131, 702413, 702431, 705079, 705097, 705613, 705631, 708091, 708109, 711479, 711497, 716713, 716731, 719839, 719893, 720913, 720931, 724313, 724331, 728813, 728831, 732079, 732097, 732713, 732731, 734113, 734131, 734479, 734497, 741413, 741431, 743279, 743297, 747713, 747731, 749279, 749297, 752413, 752431, 754513, 754531, 759113, 759131, 761713, 761731, 761879, 761897, 765913, 765931, 771091, 771109, 772279, 772297, 773879, 773897, 777013, 777031, 778579, 778597, 780613, 780631, 786179, 786197, 788213, 788231, 788479, 788497, 790379, 790397, 792713, 792731, 793279, 793297, 800879, 800897, 802037, 802073, 807017, 807071, 809213, 809231, 809779, 809797.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 1276660 values, from 1913 to 1999996897).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 0 | 1276660 | 2 | ||||||||
| 3 | 0 | 639402 | 637258 | 3 | |||||||
| 4 | 0 | 709934 | 0 | 566726 | 4 | ||||||
| 5 | 0 | 299207 | 346851 | 340015 | 290587 | 5 | |||||
| 6 | 0 | 639402 | 0 | 0 | 0 | 637258 | 6 | ||||
| 7 | 0 | 233953 | 242531 | 161518 | 161737 | 243035 | 233886 | 7 | |||
| 8 | 0 | 344806 | 0 | 290208 | 0 | 365128 | 0 | 276518 | 8 | ||
| 9 | 0 | 212752 | 213111 | 0 | 212844 | 212260 | 0 | 213806 | 211887 | 9 | |
| 10 | 0 | 299207 | 0 | 340015 | 0 | 0 | 0 | 346851 | 0 | 290587 | 10 |
| 11 | 0 | 138547 | 135590 | 134801 | 91526 | 138090 | 137676 | 91670 | 134402 | 135200 | 139158 |
A pictorial representation of the table above
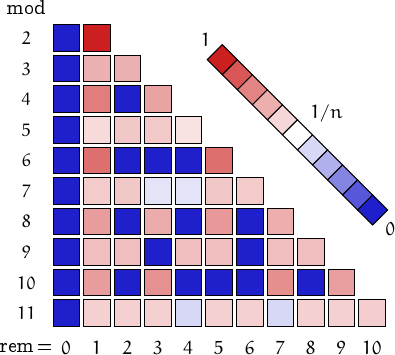
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits