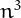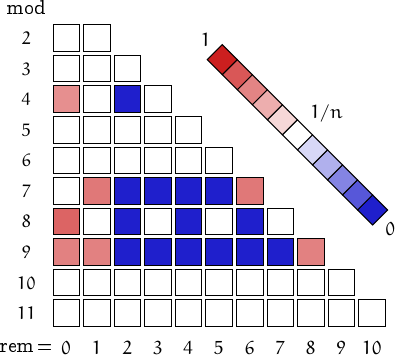
.
Every sufficiently large number can be written as the sum of at most 7 positive cubes. Nine cubes are needed only for 9 and 239 and eight cubes are needed for 15 numbers, the largest being 454.
It is not presently know if for all
sufficiently large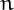 
less than 7 cubes are enough:
8042 is the
largest known number which needs 7 cubes and Deshouillers et al. in
2000 conjectured
that 7373170279850 is the
largest integer that cannot be expressed as the sum of 4
nonnegative cubes.
Every multiple of 6 can be represented as a sum of 4 signed cubes, since
![\[6n=(n+1)^3+(n-1)^3-n^3-n^3.\]](pic.3.png)
Mahler proved that 1 has infinitely many representations as 3 signed cubes.
Every cube is the difference between the squares of two consecutive
triangular numbers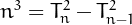 
.
There is only one known palindromic cube whose base is not palindromic, i.e., 22013 = 10662526601.
The formula
![\[n+\left\lfloor%
\sqrt[3]{n+\sqrt[3]{n}}
\right\rfloor
\]](pic.5.png)
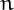-th non-cube.
The first cubic numbers are 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197, 2744, 3375, 4096, 4913, 5832, 6859, 8000 more terms
