A number 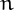 is called sliding if there exists
two numbers
is called sliding if there exists
two numbers 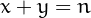 such that
such that
![\[
\frac{1}{x}+\frac{1}{y} = \frac{n}{10^k}
\]](pic.3.png) for some
for some 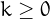 . Note that
. Note that 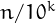 is simply
is simply 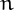 "shifted" by
"shifted" by 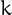 decimal places.
decimal places.
![\[
\frac{1}{256000}+\frac{1}{390625}=0.00000646625\,.
\]](pic.10.png)
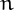 is called sliding if there exists
two numbers
is called sliding if there exists
two numbers 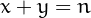 such that
such that
![\[
\frac{1}{x}+\frac{1}{y} = \frac{n}{10^k}
\]](pic.3.png)
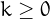 . Note that
. Note that 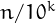 is simply
is simply 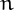 "shifted" by
"shifted" by 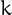 decimal places.
decimal places.
For example, 7 is a sliding number because 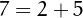 and
and 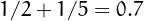 .
Similarly, 646625 is a sliding number because
.
Similarly, 646625 is a sliding number because 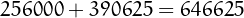 and
and
![\[
\frac{1}{256000}+\frac{1}{390625}=0.00000646625\,.
\]](pic.10.png)
In practice, a number 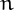 is sliding if it can be written as
is sliding if it can be written as 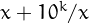 for some
for some 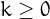 , where
, where 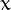 is a divisor of
is a divisor of 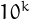 . The sliding numbers which are not divisible by 10 are called primitive sliding numbers.
. The sliding numbers which are not divisible by 10 are called primitive sliding numbers.
Up to 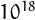 there are only 3861 sliding numbers.
there are only 3861 sliding numbers.
The first sliding numbers are 2, 7, 11, 20, 25, 29, 52, 65, 70, 101, 110, 133, 200, 205, 250, 254, 290, 425, 502, 520, 641, 650 more terms
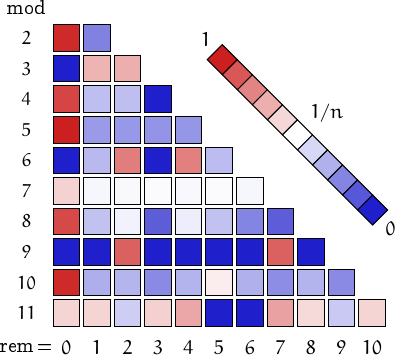
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

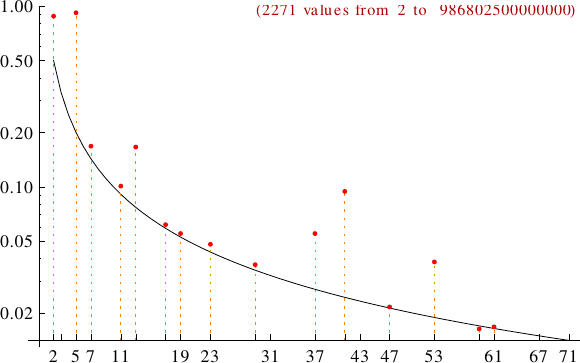
A graph displaying how many sliding numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Sliding numbers can also be... (you may click on names or numbers and on + to get more values)
a-pointer
11
101
ABA
200
2500
20000
+
2000000000000
aban
11
20
25
+
925000000000
abundant
20
70
200
+
42500000
Achilles
200
2000
20000
+
20000000000000
admirable
20
70
650
alt.fact.
101
alternating
25
29
52
+
490329250
amenable
20
25
29
+
986802500
amicable
5020
apocalyptic
650
700
925
+
29000
arithmetic
11
20
29
+
9868025
automorphic
25
Bell
52
binomial
20
70
1001
1330
brilliant
25
c.decagonal
11
101
c.octagonal
25
c.square
25
925
3445
Chen
11
29
101
641
congruent
20
29
52
+
9250000
constructible
20
Cullen
25
65
Cunningham
65
101
290
+
100000000000001
Curzon
29
65
254
+
97666490
cyclic
11
29
65
+
9766649
d-powerful
2225
22025
62660
+
3231250
de Polignac
10001
48830173
decagonal
52
deceptive
10001
100001
100000001
10000000001
deficient
11
25
29
+
9868025
dig.balanced
11
52
290
+
195824500
Duffinian
25
65
133
+
9868025
eban
52
2000
2050
+
52000000000000
economical
11
25
29
+
20000000
emirpimes
205
502
16265
+
3906506
enlightened
250
2500
25000
+
250000000000
equidigital
11
25
29
+
16265000
eRAP
20
esthetic
65
101
1010
Eulerian
11
502
evil
20
29
65
+
1000000001
Friedman
25
2500
2504
+
393185
frugal
20000
25000
160625
+
925000000
gapful
110
200
700
+
81250000000
Gilda
29
110
good prime
11
29
101
641
happy
70
133
700
+
9775865
Harshad
20
70
110
+
9250000000
hoax
250
650
2500
+
78500000
Hogben
133
iban
11
20
70
+
700000
idoneal
25
70
133
520
inconsummate
65
650
785
+
785000
interprime
205
254
650
+
97657274
Jacobsthal
11
junction
101
925
1001
+
97758650
katadrome
20
52
65
+
6410
Lehmer
133
Leyland
20000000000
Lucas
11
29
lucky
25
133
205
+
7073125
magic
65
magnanimous
11
20
25
+
2225
metadrome
25
29
1258
15689
modest
29
133
6266
Moran
133
15689
90925
1563140
nialpdrome
11
20
52
+
700000000000000
nude
11
O'Halloran
20
oban
11
20
25
+
925
octagonal
65
133
odious
11
25
52
+
976664900
palindromic
11
101
1001
+
100000000000001
palprime
11
101
pancake
11
29
254
panconsummate
11
20
pandigital
11
16265
200432500
partition
11
101
pentagonal
70
425
925
1001
pernicious
11
20
25
+
9868025
Perrin
29
plaindrome
11
25
29
+
15689
power
25
2500
250000
+
25000000000000
powerful
25
200
2000
+
250000000000000
practical
20
200
520
+
9250000
prim.abundant
20
70
650
prime
11
29
101
641
pronic
20
110
650
+
100000010000000
Proth
25
65
641
pseudoperfect
20
200
520
+
925000
rare
65
repdigit
11
repunit
133
Ruth-Aaron
25
1330
self
20
110
3157
+
250000004
semiprime
25
65
133
+
10000001
Smith
62660
Sophie Germain
11
29
641
sphenic
70
110
290
+
48830173
square
25
2500
250000
+
25000000000000
strobogrammatic
11
101
1001
+
100000000000001
strong prime
11
29
101
641
super Niven
20
70
110
+
20000050000
super-d
15689
78253
156890
+
7825300
tau
2000
2504
25040
+
801250000
tetrahedral
20
1330
tetranacci
29
trimorphic
25
truncatable prime
29
twin
11
29
101
641
uban
11
20
25
+
70000000000000
Ulam
11
502
5020
+
6415625
undulating
101
1010
unprimeable
200
1330
6410
+
9775865
untouchable
52
290
520
+
785000
wasteful
20
52
65
+
9868025
weird
70
Zuckerman
11
Zumkeller
20
70
520
+
92500
zygodrome
11
1100
11000
+
110000000000000