Search a number
Motzkin numbers

Search a number

(max 15 digits)

Numbers which count the ways in which it is possible to draw non-intersecting chords between n points on a circle. more

The Motzkin numbers up to 1015 :
1, 2, 4, 9, 21, 51, 127, 323, 835, 2188, 5798, 15511, 41835, 113634, 310572, 853467, 2356779, 6536382, 18199284, 50852019, 142547559, 400763223, 1129760415, 3192727797, 9043402501, 25669818476, 73007772802, 208023278209, 593742784829, 1697385471211, 4859761676391, 13933569346707, 40002464776083, 114988706524270, 330931069469828, 953467954114363.

Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 100000 values, from 1 to 6.2⋅1047704).

n\r 0  1 
23333266668 2 
39693120461023 3 
416666333341666633334 4 
51000022474224912250622529 5 
632296136435464635682669 6 
755270745875457545737573747433 7 
80167488333167001666616586833316634 8 
99001956034125608033404352683342 9 
1033351464470801544880296665783015411705814500 10 
11181998309577976610008966099619773981198209975

A pictorial representation of the table above
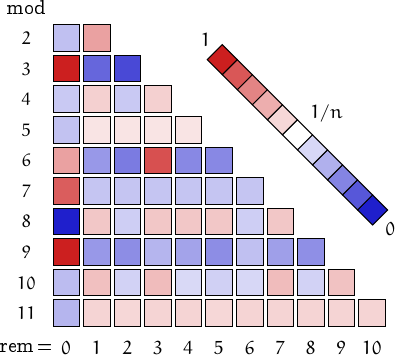
motab
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.