The automorphic numbers up to 1015 :
1, 5, 6, 25, 76, 376, 625, 9376, 90625, 109376, 890625, 2890625, 7109376, 12890625, 87109376, 212890625, 787109376, 1787109376, 8212890625, 18212890625, 81787109376, 918212890625, 9918212890625, 40081787109376, 59918212890625, 259918212890625, 740081787109376.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 27 values, from 1 to 740081787109376).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 12 | 15 | 2 | ||||||||
| 3 | 7 | 11 | 9 | 3 | |||||||
| 4 | 11 | 15 | 1 | 0 | 4 | ||||||
| 5 | 14 | 13 | 0 | 0 | 0 | 5 | |||||
| 6 | 4 | 6 | 3 | 3 | 5 | 6 | 6 | ||||
| 7 | 1 | 4 | 4 | 5 | 4 | 5 | 4 | 7 | |||
| 8 | 10 | 14 | 0 | 0 | 1 | 1 | 1 | 0 | 8 | ||
| 9 | 0 | 1 | 0 | 3 | 5 | 4 | 4 | 5 | 5 | 9 | |
| 10 | 0 | 1 | 0 | 0 | 0 | 14 | 12 | 0 | 0 | 0 | 10 |
| 11 | 1 | 4 | 3 | 3 | 1 | 3 | 3 | 1 | 3 | 2 | 3 |
A pictorial representation of the table above
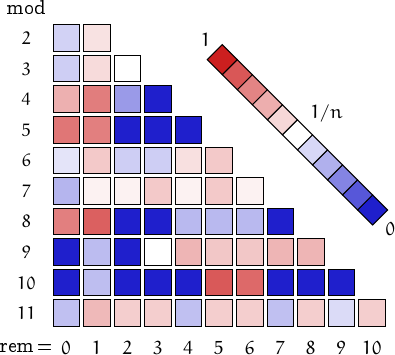
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits