• 25 can be written using four 4's:
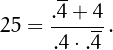
25 has 3 divisors (see below), whose sum is σ = 31. Its totient is φ = 20.
The previous prime is 23. The next prime is 29. The reversal of 25 is 52.
The square root of 25 is 5.
It is a perfect power (a square), and thus also a powerful number.
25 is nontrivially palindromic in base 4.
25 is an esthetic number in base 4, base 7, base 11 and base 12, because in such bases its adjacent digits differ by 1.
It is a semiprime because it is the product of two primes, and also a brilliant number, because the two primes have the same length.
It can be written as a sum of positive squares in only one way, i.e., 9 + 16 = 3^2 + 4^2 .
It is a sliding number, since 25 = 5 + 20 and 1/5 + 1/20 = 0.25.
It is a Cullen number, since it is equal to 3×23+1.
It is an automorphic number since its square, 625, ends in 25.
It is a trimorphic number since its cube, 15625, ends in 25.
It is not a de Polignac number, because 25 - 21 = 23 is a prime.
25 is an idoneal number.
It is a magnanimous number.
It is an alternating number because its digits alternate between even and odd.
It is a Duffinian number.
25 is an undulating number in base 4.
Its product of digits (10) is a multiple of the sum of its prime divisors (5).
25 is a lucky number.
It is a plaindrome in base 7, base 9, base 10, base 11, base 13, base 14, base 15 and base 16.
It is a nialpdrome in base 3, base 5, base 6, base 8 and base 12.
It is a pernicious number, because its binary representation contains a prime number (3) of ones.
It is a polite number, since it can be written in 2 ways as a sum of consecutive naturals, for example, 3 + ... + 7.
25 is a Friedman number, since it can be written as 5^2, using all its digits and the basic arithmetic operations.
It is a Proth number, since it is equal to 3 ⋅ 23 + 1 and 3 < 23.
25 is the 5-th square number.
25 is the 4-th centered square number and also the 3-rd centered octagonal number.
It is an amenable number.
25 is a deficient number, since it is larger than the sum of its proper divisors (6).
25 is an equidigital number, since it uses as much as digits as its factorization.
With its predecessor (24) it forms an eRAP, since the sums of their prime factors are consecutive (9 and 10).
With its predecessor (24) it forms a Ruth-Aaron pair, since the sum of their distinct prime factors is the same (5).
25 is an odious number, because the sum of its binary digits is odd.
The sum of its prime factors is 10 (or 5 counting only the distinct ones).
The product of its digits is 10, while the sum is 7.
The cubic root of 25 is about 2.9240177382.
Subtracting from 25 its product of digits (10), we obtain a triangular number (15 = T5).
Adding to 25 its reverse (52), we get a palindrome (77).
Subtracting 25 from its reverse (52), we obtain a cube (27 = 33).
The spelling of 25 in words is "twenty-five", and thus it is an aban number, an oban number, and an uban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.077 sec. • engine limits •

