Search a number
primeval numbers

Search a number

(max 15 digits)

A number that sets a record for the number of distinct primes that can be written using its digits. more

The primeval numbers up to 1.01×1011 :
1, 2, 13, 37, 107, 113, 137, 1013, 1037, 1079, 1237, 1367, 1379, 10079, 10123, 10136, 10139, 10237, 10279, 10367, 10379, 12379, 13679, 100279, 100379, 101237, 102347, 102379, 103679, 123479, 1001237, 1002347, 1002379, 1003679, 1012349, 1012379, 1023457, 1023467, 1023479, 1234579, 1234679, 10012349, 10012379, 10023457, 10023467, 10023479, 10034579, 10123457, 10123469, 10123579, 10123679, 10234567, 10234579, 10234679, 12345679, 100123379, 100123457, 100123469, 100123579, 100123679, 100233479, 100234567, 100234579, 100234679, 101234567, 101234579, 102334679, 102345679, 1000234579, 1000234679, 1001233469, 1001233579, 1001233679, 1001234567, 1001234579, 1002334679, 1002345679, 1012345678, 1012345679, 1123456789, 10001234579, 10002334679, 10002345679, 10012234579, 10012234679, 10012334579, 10012345678, 10012345679, 10122345679, 10123345679, 10123456789, 100012345678, 100012345679, 100112345678, 100112345789, 100122345679, 100123345679, 100123456789, 101233456789, 101234567789.

Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 100 values, from 1 to 101234567789).

n\r 0  1 
2694 2 
303664 3 
4126568 4 
50223867 5 
603330361 6 
714131315121419 7 
817129019439 8 
901820016220222 9 
10011400122467 10 
11034172324188300

A pictorial representation of the table above
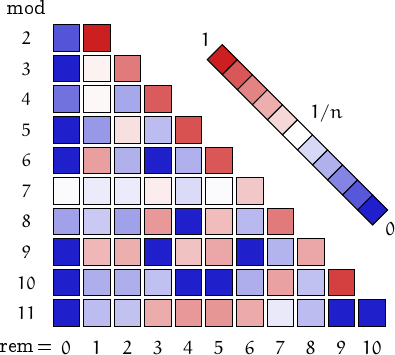
motab
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.