The first 600 self-describing numbers :
22, 4444, 224444, 442244, 444422, 666666, 10123133, 10123331, 10143133, 10143331, 10153133, 10153331, 10163133, 10163331, 10173133, 10173331, 10183133, 10183331, 10193133, 10193331, 10212332, 10213223, 10232132, 10233221, 10311233, 10311433, 10311533, 10311633, 10311733, 10311833, 10311933, 10313312, 10313314, 10313315, 10313316, 10313317, 10313318, 10313319, 10322123, 10322321, 10331231, 10331431, 10331531, 10331631, 10331731, 10331831, 10331931, 10333112, 10333114, 10333115, 10333116, 10333117, 10333118, 10333119, 12103133, 12103331, 12143133, 12143331, 12153133, 12153331, 12163133, 12163331, 12173133, 12173331, 12183133, 12183331, 12193133, 12193331, 12311033, 12311433, 12311533, 12311633, 12311733, 12311833, 12311933, 12313310, 12313314, 12313315, 12313316, 12313317, 12313318, 12313319, 12331031, 12331431, 12331531, 12331631, 12331731, 12331831, 12331931, 12333110, 12333114, 12333115, 12333116, 12333117, 12333118, 12333119, 14103133, 14103331, 14123133, 14123331, 14153133, 14153331, 14163133, 14163331, 14173133, 14173331, 14183133, 14183331, 14193133, 14193331, 14212332, 14213223, 14232132, 14233221, 14311033, 14311233, 14311533, 14311633, 14311733, 14311833, 14311933, 14313310, 14313312, 14313315, 14313316, 14313317, 14313318, 14313319, 14322123, 14322321, 14331031, 14331231, 14331531, 14331631, 14331731, 14331831, 14331931, 14333110, 14333112, 14333115, 14333116, 14333117, 14333118, 14333119, 15103133, 15103331, 15123133, 15123331, 15143133, 15143331, 15163133, 15163331, 15173133, 15173331, 15183133, 15183331, 15193133, 15193331, 15212332, 15213223, 15232132, 15233221, 15311033, 15311233, 15311433, 15311633, 15311733, 15311833, 15311933, 15313310, 15313312, 15313314, 15313316, 15313317, 15313318, 15313319, 15322123, 15322321, 15331031, 15331231, 15331431, 15331631, 15331731, 15331831, 15331931, 15333110, 15333112, 15333114, 15333116, 15333117, 15333118, 15333119, 16103133, 16103331, 16123133, 16123331, 16143133, 16143331, 16153133, 16153331, 16173133, 16173331, 16183133, 16183331, 16193133, 16193331, 16212332, 16213223, 16232132, 16233221, 16311033, 16311233, 16311433, 16311533, 16311733, 16311833, 16311933, 16313310, 16313312, 16313314, 16313315, 16313317, 16313318, 16313319, 16322123, 16322321, 16331031, 16331231, 16331431, 16331531, 16331731, 16331831, 16331931, 16333110, 16333112, 16333114, 16333115, 16333117, 16333118, 16333119, 17103133, 17103331, 17123133, 17123331, 17143133, 17143331, 17153133, 17153331, 17163133, 17163331, 17183133, 17183331, 17193133, 17193331, 17212332, 17213223, 17232132, 17233221, 17311033, 17311233, 17311433, 17311533, 17311633, 17311833, 17311933, 17313310, 17313312, 17313314, 17313315, 17313316, 17313318, 17313319, 17322123, 17322321, 17331031, 17331231, 17331431, 17331531, 17331631, 17331831, 17331931, 17333110, 17333112, 17333114, 17333115, 17333116, 17333118, 17333119, 18103133, 18103331, 18123133, 18123331, 18143133, 18143331, 18153133, 18153331, 18163133, 18163331, 18173133, 18173331, 18193133, 18193331, 18212332, 18213223, 18232132, 18233221, 18311033, 18311233, 18311433, 18311533, 18311633, 18311733, 18311933, 18313310, 18313312, 18313314, 18313315, 18313316, 18313317, 18313319, 18322123, 18322321, 18331031, 18331231, 18331431, 18331531, 18331631, 18331731, 18331931, 18333110, 18333112, 18333114, 18333115, 18333116, 18333117, 18333119, 19103133, 19103331, 19123133, 19123331, 19143133, 19143331, 19153133, 19153331, 19163133, 19163331, 19173133, 19173331, 19183133, 19183331, 19212332, 19213223, 19232132, 19233221, 19311033, 19311233, 19311433, 19311533, 19311633, 19311733, 19311833, 19313310, 19313312, 19313314, 19313315, 19313316, 19313317, 19313318, 19322123, 19322321, 19331031, 19331231, 19331431, 19331531, 19331631, 19331731, 19331831, 19333110, 19333112, 19333114, 19333115, 19333116, 19333117, 19333118, 20202442, 20203233, 20203332, 20204224, 20242042, 20244220, 20322033, 20323320, 20332032, 20333220, 20422024, 20422420, 21102332, 21103223, 21142332, 21143223, 21152332, 21153223, 21162332, 21163223, 21172332, 21173223, 21182332, 21183223, 21192332, 21193223, 21212442, 21213233, 21213332, 21214224, 21231032, 21231432, 21231532, 21231632, 21231732, 21231832, 21231932, 21233210, 21233214, 21233215, 21233216, 21233217, 21233218, 21233219, 21242142, 21244221, 21321023, 21321423, 21321523, 21321623, 21321723, 21321823, 21321923, 21322133, 21322310, 21322314, 21322315, 21322316, 21322317, 21322318, 21322319, 21323321, 21332132, 21333221, 21422124, 21422421, 22666666, 23102132, 23103221, 23142132, 23143221, 23152132, 23153221, 23162132, 23163221, 23172132, 23173221, 23182132, 23183221, 23192132, 23193221, 23211032, 23211432, 23211532, 23211632, 23211732, 23211832, 23211932, 23213210, 23213214, 23213215, 23213216, 23213217, 23213218, 23213219, 23232442, 23234224, 23242342, 23244223, 23321021, 23321421, 23321521, 23321621, 23321721, 23321821, 23321921, 23322110, 23322114, 23322115, 23322116, 23322117, 23322118, 23322119, 23422324, 23422423, 24202042, 24204220, 24212142, 24214221, 24232342, 24234223, 24243233, 24243332, 24252542, 24254225, 24262642, 24264226, 24272742, 24274227, 24282842, 24284228, 24292942, 24294229, 24322433, 24323324, 24332432, 24333224, 24422020, 24422121, 24422323, 24422525, 24422626, 24422727, 24422828, 24422929, 25242542, 25244225, 25252442, 25253233, 25253332, 25254224, 25322533, 25323325, 25332532, 25333225, 25422425, 25422524, 26242642, 26244226, 26262442, 26263233, 26263332, 26264224, 26322633, 26323326, 26332632, 26333226, 26422426, 26422624, 27242742, 27244227, 27272442, 27273233, 27273332, 27274224, 27322733, 27323327, 27332732, 27333227, 27422427, 27422724, 28242842, 28244228, 28282442, 28283233, 28283332, 28284224, 28322833, 28323328, 28332832, 28333228, 28422428, 28422824, 29242942, 29244229, 29292442, 29293233, 29293332, 29294224, 29322933, 29323329, 29332932, 29333229, 29422429, 29422924, 31101233, 31101433, 31101533, 31101633, 31101733, 31101833, 31101933, 31103312, 31103314, 31103315, 31103316.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 783343 values, from 22 to 88888888666666).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 339443 | 443900 | 2 | ||||||||
| 3 | 259975 | 265258 | 258110 | 3 | |||||||
| 4 | 155477 | 148722 | 183966 | 295178 | 4 | ||||||
| 5 | 149320 | 202255 | 144305 | 150415 | 137048 | 5 | |||||
| 6 | 111960 | 149474 | 111699 | 148015 | 115784 | 146411 | 6 | ||||
| 7 | 111488 | 111705 | 112136 | 110476 | 111953 | 111562 | 114023 | 7 | |||
| 8 | 74455 | 76347 | 87928 | 137471 | 81022 | 72375 | 96038 | 157707 | 8 | ||
| 9 | 96640 | 110964 | 90006 | 84498 | 70061 | 66803 | 78837 | 84233 | 101301 | 9 | |
| 10 | 43990 | 144260 | 100315 | 106330 | 93058 | 105330 | 57995 | 43990 | 44085 | 43990 | 10 |
| 11 | 77380 | 79155 | 68460 | 61596 | 62202 | 62238 | 68211 | 66330 | 77352 | 82224 | 78195 |
A pictorial representation of the table above
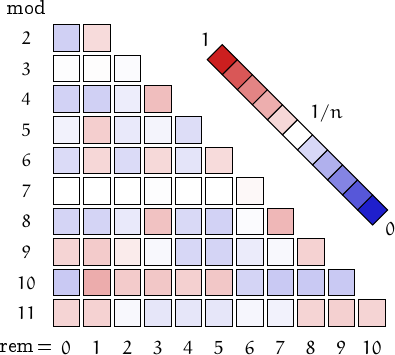
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits