Search a number
Perrin numbers

Search a number

(max 15 digits)

Numbers defined by the recurrence P(0)=3, P(1)=0, P(2)=2 and P(n) = P(n-2) + P(n-3). more

The Perrin numbers up to 1015 :
2, 3, 5, 7, 10, 12, 17, 22, 29, 39, 51, 68, 90, 119, 158, 209, 277, 367, 486, 644, 853, 1130, 1497, 1983, 2627, 3480, 4610, 6107, 8090, 10717, 14197, 18807, 24914, 33004, 43721, 57918, 76725, 101639, 134643, 178364, 236282, 313007, 414646, 549289, 727653, 963935, 1276942, 1691588, 2240877, 2968530, 3932465, 5209407, 6900995, 9141872, 12110402, 16042867, 21252274, 28153269, 37295141, 49405543, 65448410, 86700684, 114853953, 152149094, 201554637, 267003047, 353703731, 468557684, 620706778, 822261415, 1089264462, 1442968193, 1911525877, 2532232655, 3354494070, 4443758532, 5886726725, 7798252602, 10330485257, 13684979327, 18128737859, 24015464584, 31813717186, 42144202443, 55829181770, 73957919629, 97973384213, 129787101399, 171931303842, 227760485612, 301718405241, 399691789454, 529478890853, 701410194695, 929170680307, 1230889085548, 1630580875002, 2160059765855, 2861469960550, 3790640640857, 5021529726405, 6652110601407, 8812170367262, 11673640327812, 15464280968669, 20485810695074, 27137921296481, 35950091663743, 47623731991555, 63088012960224, 83573823655298, 110711744951779, 146661836615522, 194285568607077, 257373581567301, 340947405222599, 451659150174378, 598320986789900, 792606555396977.

Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 100000 values, from 2 to 2.2⋅1012212).

n\r 0  1 
24285857142 2 
3307702307646154 3 
414286285722857228570 4 
5208358333333341666620832 5 
613188131871978117582988926373 6 
712500125001250116667124991666816665 7 
8357210714178581071410714178581071417856 8 
976935128179501538551281794876921282010256 9 
1089324762142849523892811903357119050714311904 10 
1191671416411669833411666916641699168666666669165

A pictorial representation of the table above
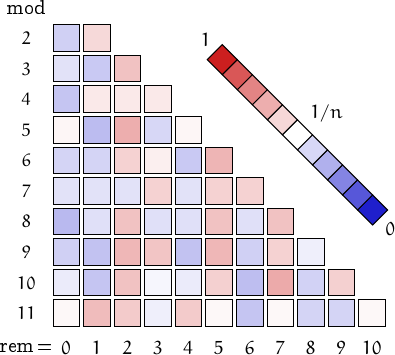
motab
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.