The first 600 strobogrammatic numbers :
1, 8, 11, 69, 88, 96, 101, 111, 181, 609, 619, 689, 808, 818, 888, 906, 916, 986, 1001, 1111, 1691, 1881, 1961, 6009, 6119, 6699, 6889, 6969, 8008, 8118, 8698, 8888, 8968, 9006, 9116, 9696, 9886, 9966, 10001, 10101, 10801, 11011, 11111, 11811, 16091, 16191, 16891, 18081, 18181, 18881, 19061, 19161, 19861, 60009, 60109, 60809, 61019, 61119, 61819, 66099, 66199, 66899, 68089, 68189, 68889, 69069, 69169, 69869, 80008, 80108, 80808, 81018, 81118, 81818, 86098, 86198, 86898, 88088, 88188, 88888, 89068, 89168, 89868, 90006, 90106, 90806, 91016, 91116, 91816, 96096, 96196, 96896, 98086, 98186, 98886, 99066, 99166, 99866, 100001, 101101, 106901, 108801, 109601, 110011, 111111, 116911, 118811, 119611, 160091, 161191, 166991, 168891, 169691, 180081, 181181, 186981, 188881, 189681, 190061, 191161, 196961, 198861, 199661, 600009, 601109, 606909, 608809, 609609, 610019, 611119, 616919, 618819, 619619, 660099, 661199, 666999, 668899, 669699, 680089, 681189, 686989, 688889, 689689, 690069, 691169, 696969, 698869, 699669, 800008, 801108, 806908, 808808, 809608, 810018, 811118, 816918, 818818, 819618, 860098, 861198, 866998, 868898, 869698, 880088, 881188, 886988, 888888, 889688, 890068, 891168, 896968, 898868, 899668, 900006, 901106, 906906, 908806, 909606, 910016, 911116, 916916, 918816, 919616, 960096, 961196, 966996, 968896, 969696, 980086, 981186, 986986, 988886, 989686, 990066, 991166, 996966, 998866, 999666, 1000001, 1001001, 1008001, 1010101, 1011101, 1018101, 1060901, 1061901, 1068901, 1080801, 1081801, 1088801, 1090601, 1091601, 1098601, 1100011, 1101011, 1108011, 1110111, 1111111, 1118111, 1160911, 1161911, 1168911, 1180811, 1181811, 1188811, 1190611, 1191611, 1198611, 1600091, 1601091, 1608091, 1610191, 1611191, 1618191, 1660991, 1661991, 1668991, 1680891, 1681891, 1688891, 1690691, 1691691, 1698691, 1800081, 1801081, 1808081, 1810181, 1811181, 1818181, 1860981, 1861981, 1868981, 1880881, 1881881, 1888881, 1890681, 1891681, 1898681, 1900061, 1901061, 1908061, 1910161, 1911161, 1918161, 1960961, 1961961, 1968961, 1980861, 1981861, 1988861, 1990661, 1991661, 1998661, 6000009, 6001009, 6008009, 6010109, 6011109, 6018109, 6060909, 6061909, 6068909, 6080809, 6081809, 6088809, 6090609, 6091609, 6098609, 6100019, 6101019, 6108019, 6110119, 6111119, 6118119, 6160919, 6161919, 6168919, 6180819, 6181819, 6188819, 6190619, 6191619, 6198619, 6600099, 6601099, 6608099, 6610199, 6611199, 6618199, 6660999, 6661999, 6668999, 6680899, 6681899, 6688899, 6690699, 6691699, 6698699, 6800089, 6801089, 6808089, 6810189, 6811189, 6818189, 6860989, 6861989, 6868989, 6880889, 6881889, 6888889, 6890689, 6891689, 6898689, 6900069, 6901069, 6908069, 6910169, 6911169, 6918169, 6960969, 6961969, 6968969, 6980869, 6981869, 6988869, 6990669, 6991669, 6998669, 8000008, 8001008, 8008008, 8010108, 8011108, 8018108, 8060908, 8061908, 8068908, 8080808, 8081808, 8088808, 8090608, 8091608, 8098608, 8100018, 8101018, 8108018, 8110118, 8111118, 8118118, 8160918, 8161918, 8168918, 8180818, 8181818, 8188818, 8190618, 8191618, 8198618, 8600098, 8601098, 8608098, 8610198, 8611198, 8618198, 8660998, 8661998, 8668998, 8680898, 8681898, 8688898, 8690698, 8691698, 8698698, 8800088, 8801088, 8808088, 8810188, 8811188, 8818188, 8860988, 8861988, 8868988, 8880888, 8881888, 8888888, 8890688, 8891688, 8898688, 8900068, 8901068, 8908068, 8910168, 8911168, 8918168, 8960968, 8961968, 8968968, 8980868, 8981868, 8988868, 8990668, 8991668, 8998668, 9000006, 9001006, 9008006, 9010106, 9011106, 9018106, 9060906, 9061906, 9068906, 9080806, 9081806, 9088806, 9090606, 9091606, 9098606, 9100016, 9101016, 9108016, 9110116, 9111116, 9118116, 9160916, 9161916, 9168916, 9180816, 9181816, 9188816, 9190616, 9191616, 9198616, 9600096, 9601096, 9608096, 9610196, 9611196, 9618196, 9660996, 9661996, 9668996, 9680896, 9681896, 9688896, 9690696, 9691696, 9698696, 9800086, 9801086, 9808086, 9810186, 9811186, 9818186, 9860986, 9861986, 9868986, 9880886, 9881886, 9888886, 9890686, 9891686, 9898686, 9900066, 9901066, 9908066, 9910166, 9911166, 9918166, 9960966, 9961966, 9968966, 9980866, 9981866, 9988866, 9990666, 9991666, 9998666, 10000001, 10011001, 10069001, 10088001, 10096001, 10100101, 10111101, 10169101, 10188101, 10196101, 10600901, 10611901, 10669901, 10688901, 10696901, 10800801, 10811801, 10869801, 10888801, 10896801, 10900601, 10911601, 10969601, 10988601, 10996601, 11000011, 11011011, 11069011, 11088011, 11096011, 11100111, 11111111, 11169111, 11188111, 11196111, 11600911, 11611911, 11669911, 11688911, 11696911, 11800811, 11811811, 11869811, 11888811, 11896811, 11900611, 11911611, 11969611, 11988611, 11996611, 16000091, 16011091, 16069091, 16088091, 16096091, 16100191, 16111191, 16169191, 16188191, 16196191, 16600991, 16611991, 16669991, 16688991, 16696991, 16800891, 16811891, 16869891, 16888891, 16896891, 16900691, 16911691, 16969691, 16988691, 16996691, 18000081, 18011081, 18069081, 18088081, 18096081, 18100181, 18111181, 18169181, 18188181, 18196181, 18600981, 18611981, 18669981, 18688981, 18696981, 18800881, 18811881, 18869881, 18888881, 18896881, 18900681, 18911681, 18969681, 18988681, 18996681, 19000061, 19011061.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 312498 values, from 1 to 999999986666666).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 156249 | 156249 | 2 | ||||||||
| 3 | 104250 | 104124 | 104124 | 3 | |||||||
| 4 | 78126 | 93750 | 78123 | 62499 | 4 | ||||||
| 5 | 0 | 156249 | 0 | 78125 | 78124 | 5 | |||||
| 6 | 52125 | 51999 | 51999 | 52125 | 52125 | 52125 | 6 | ||||
| 7 | 53536 | 29021 | 50682 | 60408 | 30065 | 28831 | 59955 | 7 | |||
| 8 | 43754 | 50003 | 40624 | 37500 | 34372 | 43747 | 37499 | 24999 | 8 | ||
| 9 | 34538 | 34322 | 34769 | 35148 | 34821 | 34403 | 34564 | 34981 | 34952 | 9 | |
| 10 | 0 | 78125 | 0 | 0 | 0 | 0 | 78124 | 0 | 78125 | 78124 | 10 |
| 11 | 39458 | 22551 | 25188 | 37453 | 21874 | 31028 | 30411 | 21494 | 36482 | 24619 | 21940 |
A pictorial representation of the table above
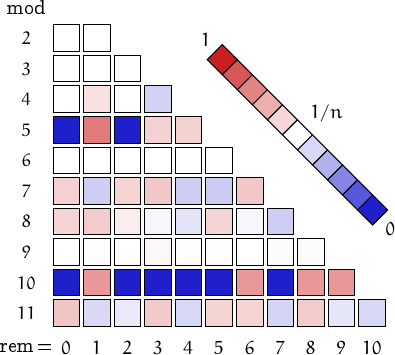
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits