• 96 can be written using four 4's:
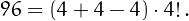
96 has 12 divisors (see below), whose sum is σ = 252. Its totient is φ = 32.
The previous prime is 89. The next prime is 97. The reversal of 96 is 69.
It is a Jordan-Polya number, since it can be written as 4! ⋅ (2!)2.
96 is nontrivially palindromic in base 11 and base 15.
It is a tau number, because it is divible by the number of its divisors (12).
It is an alternating number because its digits alternate between odd and even.
96 is a strobogrammatic number because it is the same when read upside-down.
96 is a nontrivial repdigit in base 11 and base 15.
It is a plaindrome in base 9, base 11, base 14 and base 15.
It is a nialpdrome in base 2, base 10, base 11, base 12, base 13, base 15 and base 16.
It is a zygodrome in base 2, base 11 and base 15.
It is a congruent number.
96 is an untouchable number, because it is not equal to the sum of proper divisors of any number.
It is a pernicious number, because its binary representation contains a prime number (2) of ones.
In principle, a polygon with 96 sides can be constructed with ruler and compass.
It is a polite number, since it can be written as a sum of consecutive naturals, namely, 31 + 32 + 33.
It is an arithmetic number, because the mean of its divisors is an integer number (21).
96 is the 6-th octagonal number.
It is an amenable number.
It is a practical number, because each smaller number is the sum of distinct divisors of 96, and also a Zumkeller number, because its divisors can be partitioned in two sets with the same sum (126).
96 is an abundant number, since it is smaller than the sum of its proper divisors (156).
It is a pseudoperfect number, because it is the sum of a subset of its proper divisors.
96 is a wasteful number, since it uses less digits than its factorization.
96 is an evil number, because the sum of its binary digits is even.
The sum of its prime factors is 13 (or 5 counting only the distinct ones).
The product of its digits is 54, while the sum is 15.
The square root of 96 is about 9.7979589711. The cubic root of 96 is about 4.5788569702.
Adding to 96 its sum of digits (15), we get a palindrome (111).
Subtracting from 96 its sum of digits (15), we obtain a 4-th power (81 = 34).
Multiplying 96 by its product of digits (54), we get a square (5184 = 722).
Subtracting from 96 its reverse (69), we obtain a cube (27 = 33).
The spelling of 96 in words is "ninety-six", and thus it is an aban number, an oban number, and an uban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.047 sec. • engine limits •

