Search a number
tribonacci numbers

Search a number

(max 15 digits)

Fibonacci-like numbers defined by the recurrence T(1)=T(2)=1, T(3)=2 and T(n) = T(n-1) + T(n-2) + T(n-3). more

The tribonacci numbers up to 1015 :
1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, 927, 1705, 3136, 5768, 10609, 19513, 35890, 66012, 121415, 223317, 410744, 755476, 1389537, 2555757, 4700770, 8646064, 15902591, 29249425, 53798080, 98950096, 181997601, 334745777, 615693474, 1132436852, 2082876103, 3831006429, 7046319384, 12960201916, 23837527729, 43844049029, 80641778674, 148323355432, 272809183135, 501774317241, 922906855808, 1697490356184, 3122171529233, 5742568741225, 10562230626642, 19426970897100, 35731770264967, 65720971788709, 120879712950776, 222332455004452, 408933139743937, 752145307699165.

Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 100000 values, from 1 to 2.96⋅1026464).

n\r 0  1 
25000050000 2 
3307684615523077 3 
437500375001250012500 4 
5193531935522581967829033 5 
6153842307811539153842307711538 6 
725000187501875062511875062496250 7 
825000250001250001250012500012500 8 
92307615386769301538576927692153847692 9 
1096769678112904840145199677967711291483814514 10 
1190919092909390909092909090919091909090909090

A pictorial representation of the table above
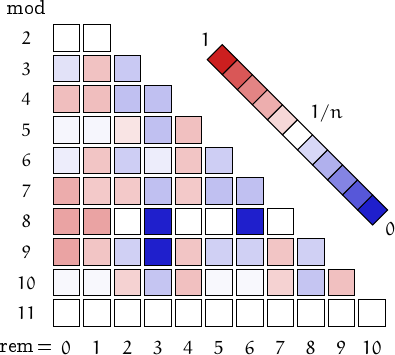
motab
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.