• 24 can be written using four 4's:
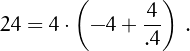
24 has 8 divisors (see below), whose sum is σ = 60. Its totient is φ = 8.
The previous prime is 23. The next prime is 29. The reversal of 24 is 42.
Added to its reverse (42) it gives a triangular number (66 = T11).
It is a factorial (24 = 4 ! = 1 ⋅ 2 ⋅ 3 ⋅ 4 ), and thus also a Jordan-Polya number.
24 is nontrivially palindromic in base 5, base 7 and base 11.
It is a Cunningham number, because it is equal to 52-1.
It is a tau number, because it is divible by the number of its divisors (8).
It is an ABA number since it can be written as A⋅BA, here for A=3, B=2.
24 is an admirable number.
It is a trimorphic number since its cube, 13824, ends in 24.
It is a Harshad number since it is a multiple of its sum of digits (6).
It is a super Niven number, because it is divisible the sum of any subset of its (nonzero) digits.
It is a nude number because it is divisible by every one of its digits and also a Zuckerman number because it is divisible by the product of its digits.
24 is an idoneal number.
It is a tribonacci number.
It is a d-powerful number, because it can be written as 42 + 23 .
It is one of the 548 Lynch-Bell numbers.
It is a compositorial, being equal to the product of composites up to 6.
24 is a nontrivial repdigit in base 5, base 7 and base 11.
It is a plaindrome in base 5, base 7, base 9, base 10, base 11, base 13, base 14, base 15 and base 16.
It is a nialpdrome in base 2, base 3, base 5, base 6, base 7, base 8, base 11 and base 12.
It is a zygodrome in base 2, base 5, base 7 and base 11.
It is a congruent number.
It is a panconsummate number.
It is a pernicious number, because its binary representation contains a prime number (2) of ones.
A polygon with 24 sides can be constructed with ruler and compass.
It is a polite number, since it can be written as a sum of consecutive naturals, namely, 7 + 8 + 9.
24 is a highly composite number, because it has more divisors than any smaller number.
24 is a superabundant number, because it has a larger abundancy index than any smaller number.
24 is the 3-rd nonagonal number.
It is an amenable number.
It is a practical number, because each smaller number is the sum of distinct divisors of 24, and also a Zumkeller number, because its divisors can be partitioned in two sets with the same sum (30).
24 is an abundant number, since it is smaller than the sum of its proper divisors (36).
It is a pseudoperfect number, because it is the sum of a subset of its proper divisors.
24 is a wasteful number, since it uses less digits than its factorization.
With its successor (25) it forms a Ruth-Aaron pair, since the sum of their distinct prime factors is the same (5).
With its successor (25) it forms an eRAP, since the sums of their prime factors are consecutive (9 and 10).
24 is an evil number, because the sum of its binary digits is even.
The sum of its prime factors is 9 (or 5 counting only the distinct ones).
The product of its digits is 8, while the sum is 6.
The square root of 24 is about 4.8989794856. The cubic root of 24 is about 2.8844991406.
Adding to 24 its reverse (42), we get a palindrome (66).
The spelling of 24 in words is "twenty-four", and thus it is an aban number and an iban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.080 sec. • engine limits •

