The first 600 frugal numbers :
125, 128, 243, 256, 343, 512, 625, 729, 1024, 1029, 1215, 1250, 1280, 1331, 1369, 1458, 1536, 1681, 1701, 1715, 1792, 1849, 1875, 2048, 2187, 2197, 2209, 2401, 2560, 2809, 3125, 3481, 3584, 3645, 3721, 4096, 4374, 4375, 4489, 4802, 4913, 5041, 5103, 5329, 6241, 6250, 6561, 6859, 6889, 7203, 7921, 8192, 9375, 9409, 10000, 10082, 10112, 10125, 10201, 10206, 10240, 10368, 10375, 10443, 10449, 10496, 10609, 10624, 10625, 10633, 10658, 10752, 10935, 10976, 10985, 11008, 11045, 11125, 11163, 11392, 11421, 11449, 11664, 11767, 11776, 11875, 11881, 11907, 12005, 12032, 12125, 12167, 12288, 12393, 12416, 12482, 12500, 12544, 12691, 12769, 12800, 12879, 12943, 13122, 13125, 13467, 13568, 13718, 13778, 13824, 13851, 14045, 14063, 14336, 14337, 14375, 14406, 14641, 14739, 14749, 14823, 14848, 15104, 15123, 15309, 15379, 15463, 15552, 15616, 15625, 15842, 15872, 15987, 16000, 16121, 16129, 16281, 16384, 16767, 16807, 16875, 17152, 17161, 17253, 17405, 17496, 17739, 17920, 18125, 18176, 18179, 18225, 18605, 18688, 18723, 18750, 18769, 18818, 18944, 19197, 19208, 19321, 19375, 19663, 19683, 20000, 20169, 20224, 20237, 20480, 20577, 20667, 20736, 20923, 20992, 21141, 21248, 21609, 21627, 21870, 21875, 21952, 22016, 22201, 22445, 22599, 22784, 22801, 22981, 23125, 23328, 23571, 23763, 24010, 24057, 24064, 24334, 24353, 24367, 24389, 24565, 24576, 24649, 24832, 25000, 25039, 25088, 25205, 25515, 25625, 26047, 26244, 26411, 26569, 26645, 26875, 26973, 27097, 27136, 27783, 27889, 28125, 28227, 28431, 28469, 28561, 28672, 29282, 29375, 29791, 29889, 29929, 30208, 30375, 30527, 30618, 30625, 31104, 31205, 31213, 31232, 31250, 31347, 31423, 32000, 32041, 32761, 32768, 32805, 33125, 33271, 33614, 34263, 34295, 34304, 34375, 34391, 34445, 34992, 35287, 35721, 36015, 36352, 36481, 36501, 36875, 37179, 37249, 37303, 37376, 38125, 38416, 38637, 38809, 39366, 39601, 39605, 40000, 40448, 40625, 40817, 40960, 41472, 41553, 41875, 42496, 42875, 43011, 43687, 43750, 43904, 43923, 44375, 44469, 44521, 45568, 45619, 45625, 45927, 46656, 46875, 47045, 48013, 48223, 48778, 48843, 49152, 49375, 49664, 49729, 50000, 50301, 50421, 50625, 50653, 51529, 51759, 51875, 52441, 52488, 53125, 53217, 54289, 54675, 55223, 55447, 55625, 57121, 57122, 57344, 57591, 58081, 59049, 59375, 59582, 60025, 60507, 60625, 60835, 62208, 62500, 63001, 63423, 64000, 64827, 64881, 65536, 65610, 65625, 65863, 66049, 67228, 67797, 68921, 69169, 69629, 69984, 70713, 71875, 72171, 72361, 73167, 73205, 73441, 74431, 76545, 76729, 76832, 78125, 78732, 78961, 79507, 80000, 80089, 80919, 81920, 83349, 83521, 84035, 84375, 85169, 85293, 85683, 85849, 87808, 88837, 89373, 89667, 90625, 91125, 91854, 93312, 93750, 94041, 94249, 96721, 96875, 97969, 98304, 98415, 98441, 100000, 100352, 100359, 100467, 100489, 100499, 100602, 100625, 100736, 100842, 100845, 100864, 100949, 101120, 101125, 101185, 101250, 101251, 101306, 101331, 101375, 101632, 101817, 101875, 101888, 102016, 102303, 102400, 102487, 102541, 102625, 102656, 102789, 102875, 102885, 102912, 102973, 103058, 103125, 103173, 103243, 103247, 103259, 103335, 103375, 103499, 103518, 103552, 103625, 103680, 103750, 103761, 103808, 103823, 103933, 103936, 104375, 104615, 104704, 104733, 104875, 104882, 104960, 104976, 105088, 105125, 105149, 105219, 105301, 105344, 105625, 105705, 105728, 105856, 105861, 106097, 106112, 106240, 106250, 106434, 106496, 106625, 106673, 106677, 107125, 107163, 107264, 107359, 107375, 107392, 107584, 107648, 107649, 107653, 107776, 107811, 107875, 107909, 107911, 108032, 108045, 108125, 108135, 108151, 108241, 108544, 108578, 108621, 108731, 108864, 109056, 109091, 109107, 109184, 109312, 109350, 109375, 109443, 109503, 109561, 109625, 109696, 109744, 109760, 109952, 110079, 110080, 110125, 110224, 110336, 110375, 110446, 110464, 110473, 110592, 110625, 110848, 110875, 110889, 110894, 111005, 111051, 111104, 111250, 111392, 111537, 111747, 111875, 111909, 112000, 112023, 112128, 112225, 112256, 112384, 112509, 112627, 112768, 112789, 112847, 112903, 112995, 112999, 113024, 113125, 113375, 113408, 113481, 113533, 113536, 113569, 113627, 113875, 113920, 113967, 114005, 114176, 114242, 114244, 114375, 114453, 114688, 114875, 114905, 114944, 115169, 115182, 115248, 115351, 115591, 115625, 115911, 115943, 116096, 116125, 116162, 116224, 116397, 116427.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 1918207 values, from 125 to 999999189).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 581431 | 1336776 | 2 | ||||||||
| 3 | 633268 | 643261 | 641678 | 3 | |||||||
| 4 | 418729 | 669539 | 162702 | 667237 | 4 | ||||||
| 5 | 495408 | 355547 | 355691 | 355831 | 355730 | 5 | |||||
| 6 | 130690 | 418915 | 226395 | 502578 | 224346 | 415283 | 6 | ||||
| 7 | 441964 | 246424 | 246490 | 245717 | 246497 | 245462 | 245653 | 7 | |||
| 8 | 398970 | 336019 | 82486 | 334800 | 19759 | 333520 | 80216 | 332437 | 8 | ||
| 9 | 493562 | 214409 | 213961 | 70532 | 214381 | 213923 | 69174 | 214471 | 213794 | 9 | |
| 10 | 109761 | 237970 | 118236 | 237580 | 117606 | 385647 | 117577 | 237455 | 118251 | 238124 | 10 |
| 11 | 55827 | 186581 | 185887 | 186641 | 186617 | 186564 | 185780 | 185865 | 185888 | 186670 | 185887 |
A pictorial representation of the table above
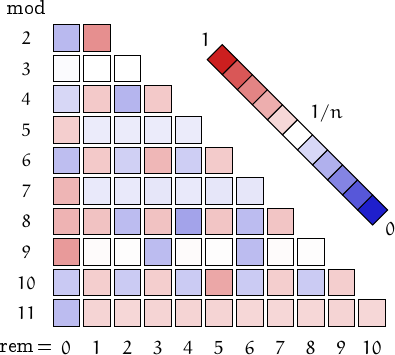
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits