The partition number up to 1015 :
1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, 792, 1002, 1255, 1575, 1958, 2436, 3010, 3718, 4565, 5604, 6842, 8349, 10143, 12310, 14883, 17977, 21637, 26015, 31185, 37338, 44583, 53174, 63261, 75175, 89134, 105558, 124754, 147273, 173525, 204226, 239943, 281589, 329931, 386155, 451276, 526823, 614154, 715220, 831820, 966467, 1121505, 1300156, 1505499, 1741630, 2012558, 2323520, 2679689, 3087735, 3554345, 4087968, 4697205, 5392783, 6185689, 7089500, 8118264, 9289091, 10619863, 12132164, 13848650, 15796476, 18004327, 20506255, 23338469, 26543660, 30167357, 34262962, 38887673, 44108109, 49995925, 56634173, 64112359, 72533807, 82010177, 92669720, 104651419, 118114304, 133230930, 150198136, 169229875, 190569292, 214481126, 241265379, 271248950, 304801365, 342325709, 384276336, 431149389, 483502844, 541946240, 607163746, 679903203, 761002156, 851376628, 952050665, 1064144451, 1188908248, 1327710076, 1482074143, 1653668665, 1844349560, 2056148051, 2291320912, 2552338241, 2841940500, 3163127352, 3519222692, 3913864295, 4351078600, 4835271870, 5371315400, 5964539504, 6620830889, 7346629512, 8149040695, 9035836076, 10015581680, 11097645016, 12292341831, 13610949895, 15065878135, 16670689208, 18440293320, 20390982757, 22540654445, 24908858009, 27517052599, 30388671978, 33549419497, 37027355200, 40853235313, 45060624582, 49686288421, 54770336324, 60356673280, 66493182097, 73232243759, 80630964769, 88751778802, 97662728555, 107438159466, 118159068427, 129913904637, 142798995930, 156919475295, 172389800255, 189334822579, 207890420102, 228204732751, 250438925115, 274768617130, 301384802048, 330495499613, 362326859895, 397125074750, 435157697830, 476715857290, 522115831195, 571701605655, 625846753120, 684957390936, 749474411781, 819876908323, 896684817527, 980462880430, 1071823774337, 1171432692373, 1280011042268, 1398341745571, 1527273599625, 1667727404093, 1820701100652, 1987276856363, 2168627105469, 2366022741845, 2580840212973, 2814570987591, 3068829878530, 3345365983698, 3646072432125, 3972999029388, 4328363658647, 4714566886083, 5134205287973, 5590088317495, 6085253859260, 6622987708040, 7206841706490, 7840656226137, 8528581302375, 9275102575355, 10085065885767, 10963707205259, 11916681236278, 12950095925895, 14070545699287, 15285151248481, 16601598107914, 18028182516671, 19573856161145, 21248279009367, 23061871173849, 25025873760111, 27152408925615, 29454549941750, 31946390696157, 34643126322519, 37561133582570, 40718063627362, 44132934884255, 47826239745920, 51820051838712, 56138148670947, 60806135438329, 65851585970275, 71304185514919, 77195892663512, 83561103925871, 90436839668817, 97862933703585, 105882246722733, 114540884553038, 123888443077259, 133978259344888, 144867692496445, 156618412527946, 169296722391554, 182973889854026, 197726516681672, 213636919820625, 230793554364681, 249291451168559, 269232701252579, 290726957916112, 313891991306665, 338854264248680, 365749566870782, 394723676655357, 425933084409356, 459545750448675, 495741934760846, 534715062908609, 576672674947168, 621837416509615, 670448123060170, 722760953690372, 779050629562167, 839611730366814, 904760108316360, 974834369944625.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 25000 values, from 1 to 7.95⋅10170).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 12604 | 12396 | 2 | ||||||||
| 3 | 8326 | 8334 | 8340 | 3 | |||||||
| 4 | 6247 | 6152 | 6357 | 6244 | 4 | ||||||
| 5 | 9121 | 3829 | 4149 | 3934 | 3967 | 5 | |||||
| 6 | 4208 | 4110 | 4172 | 4118 | 4224 | 4168 | 6 | ||||
| 7 | 6816 | 3017 | 3020 | 3072 | 3073 | 2947 | 3055 | 7 | |||
| 8 | 3133 | 3132 | 3168 | 3179 | 3114 | 3020 | 3189 | 3065 | 8 | ||
| 9 | 2775 | 2740 | 2827 | 2774 | 2753 | 2753 | 2777 | 2841 | 2760 | 9 | |
| 10 | 4679 | 1932 | 2086 | 1949 | 1957 | 4442 | 1897 | 2063 | 1985 | 2010 | 10 |
| 11 | 4425 | 2085 | 2029 | 1966 | 2111 | 2087 | 2096 | 1996 | 2133 | 2076 | 1996 |
A pictorial representation of the table above
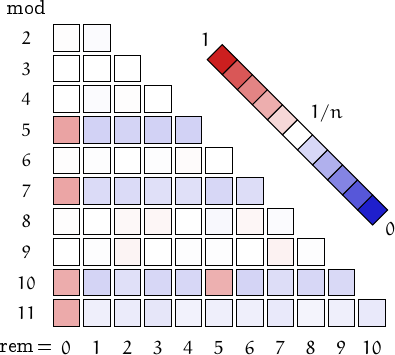
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits