The productive numbers up to 1015 :
1, 2, 4, 6, 12, 16, 22, 28, 36, 52, 58, 66, 82, 106, 112, 136, 166, 178, 256, 306, 336, 352, 448, 502, 508, 556, 562, 586, 616, 652, 658, 718, 982, 1018, 1108, 1162, 1192, 1228, 1498, 1708, 2002, 2026, 2086, 2686, 2776, 2998, 3136, 3412, 3526, 3592, 4078, 4918, 5008, 5302, 5506, 5518, 6112, 6268, 6802, 7126, 7516, 7606, 7918, 7948, 8536, 8542, 8662, 9532, 9748, 10312, 10336, 11482, 11578, 13312, 14158, 14548, 14758, 14812, 14968, 19012, 19402, 25228, 25366, 28516, 33106, 36676, 43312, 49018, 49612, 52768, 56236, 60352, 65002, 66036, 66082, 71866, 75268, 76366, 76756, 79978, 80362, 80932, 96052, 105502, 119758, 138052, 161626, 202186, 202636, 211876, 227386, 241228, 261508, 265606, 276556, 299098, 316402, 328066, 335206, 350656, 404482, 405412, 414178, 455992, 497968, 565462, 588826, 621628, 622606, 631582, 656482, 658882, 686026, 702268, 762226, 770026, 809842, 917728, 967708, 992548, 1197058, 1433512, 1577908, 1610428, 1626748, 1626958, 1651942, 1715866, 1909408, 1935442, 2460178, 2673556, 3433612, 3630952, 4764778, 5165518, 5199502, 5280616, 5538316, 6378256, 6614248, 7663156, 7929268, 8114332, 8486602, 8610442, 9109468, 9116608, 9598162, 11056216, 11311126, 11495278, 11830336, 19835602, 22067518, 23261206, 28056616, 36046162, 39933892, 44883532, 46544968, 51226666, 53486182, 60270676, 65521528, 73226356, 94150168, 114769048, 181508542, 214162078, 394166542, 656835886, 876128326, 1588350052, 1810088626, 2011703656, 2497292998, 4009910812, 4381665052, 4712920258, 5747617078, 9443049352, 9895016332, 30355578586, 45971222578, 56577109408, 80381785156, 8220001387336.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 208 values, from 1 to 8220001387336).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 207 | 1 | 2 | ||||||||
| 3 | 7 | 200 | 1 | 3 | |||||||
| 4 | 104 | 1 | 103 | 0 | 4 | ||||||
| 5 | 0 | 71 | 69 | 67 | 1 | 5 | |||||
| 6 | 7 | 1 | 1 | 0 | 199 | 0 | 6 | ||||
| 7 | 41 | 24 | 32 | 32 | 37 | 41 | 1 | 7 | |||
| 8 | 44 | 1 | 57 | 0 | 60 | 0 | 46 | 0 | 8 | ||
| 9 | 2 | 68 | 1 | 4 | 70 | 0 | 1 | 62 | 0 | 9 | |
| 10 | 0 | 1 | 69 | 0 | 1 | 0 | 70 | 0 | 67 | 0 | 10 |
| 11 | 17 | 14 | 26 | 27 | 12 | 23 | 43 | 19 | 8 | 19 | 0 |
A pictorial representation of the table above
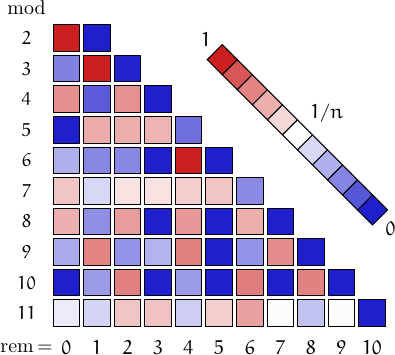
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits