The first 600 sliding numbers :
2, 7, 11, 20, 25, 29, 52, 65, 70, 101, 110, 133, 200, 205, 250, 254, 290, 425, 502, 520, 641, 650, 700, 785, 925, 1001, 1010, 1100, 1258, 1330, 2000, 2005, 2050, 2225, 2500, 2504, 2540, 2900, 3157, 3445, 4025, 4250, 5002, 5020, 5200, 6266, 6325, 6410, 6500, 7000, 7850, 8125, 9250, 10001, 10010, 10100, 11000, 12508, 12580, 13300, 15689, 16265, 16625, 20000, 20005, 20050, 20500, 22025, 22250, 25000, 25004, 25040, 25400, 29000, 31282, 31570, 34450, 35125, 40025, 40250, 42500, 50002, 50020, 50200, 52000, 62516, 62660, 63250, 64100, 65000, 70000, 78253, 78500, 79405, 79625, 80125, 81250, 90925, 92500, 100001, 100010, 100100, 101000, 110000, 125008, 125080, 125800, 133000, 156314, 156890, 160625, 162650, 166250, 200000, 200005, 200050, 200500, 205000, 206125, 220250, 222500, 250000, 250004, 250040, 250400, 254000, 290000, 312532, 312820, 315700, 323125, 344500, 351250, 390881, 393185, 400025, 400250, 402500, 416225, 425000, 500002, 500020, 500200, 502000, 520000, 625016, 625160, 626600, 632500, 641000, 646625, 650000, 655625, 700000, 781378, 782530, 785000, 794050, 796250, 800125, 801250, 812500, 909250, 925000, 1000001, 1000010, 1000100, 1001000, 1010000, 1100000, 1250008, 1250080, 1250800, 1258000, 1330000, 1358125, 1562564, 1563140, 1568900, 1600625, 1606250, 1626500, 1662500, 1953637, 1958245, 2000000, 2000005, 2000050, 2000500, 2004325, 2005000, 2050000, 2061250, 2202500, 2225000, 2465125, 2500000, 2500004, 2500040, 2500400, 2504000, 2540000, 2900000, 2950625, 3125032, 3125320, 3128200, 3157000, 3203125, 3231250, 3445000, 3512500, 3906506, 3908810, 3931850, 4000025, 4000250, 4002500, 4025000, 4162250, 4250000, 5000002, 5000020, 5000200, 5002000, 5020000, 5200000, 6250016, 6250160, 6251600, 6266000, 6325000, 6410000, 6415625, 6466250, 6500000, 6556250, 7000000, 7073125, 7812628, 7813780, 7825300, 7850000, 7940500, 7962500, 8000125, 8001250, 8012500, 8125000, 9092500, 9250000, 9766649, 9775865, 9868025, 10000001, 10000010, 10000100, 10001000, 10010000, 10100000, 10789625, 11000000, 12500008, 12500080, 12500800, 12508000, 12580000, 12878125, 13300000, 13581250, 15625064, 15625640, 15631400, 15689000, 16000625, 16006250, 16062500, 16265000, 16625000, 19531762, 19536370, 19582450, 20000000, 20000005, 20000050, 20000500, 20005000, 20005625, 20043250, 20050000, 20500000, 20612500, 22025000, 22250000, 24651250, 25000000, 25000004, 25000040, 25000400, 25004000, 25040000, 25400000, 25990625, 29000000, 29506250, 31250032, 31250320, 31253200, 31282000, 31570000, 32003125, 32031250, 32312500, 34450000, 35125000, 39062756, 39065060, 39088100, 39318500, 40000025, 40000250, 40002500, 40025000, 40250000, 41622500, 42500000, 48830173, 48848605, 49032925, 50000002, 50000020, 50000200, 50002000, 50020000, 50200000, 50876125, 52000000, 53153125, 62500016, 62500160, 62501600, 62516000, 62660000, 63250000, 64015625, 64100000, 64156250, 64662500, 65000000, 65562500, 69308125, 70000000, 70731250, 78125128, 78126280, 78137800, 78253000, 78500000, 79405000, 79625000, 80000125, 80001250, 80012500, 80125000, 81250000, 90925000, 92500000, 97657274, 97666490, 97758650, 98680250, 100000001, 100000010, 100000100, 100001000, 100010000, 100100000, 101000000, 107896250, 110000000, 112165625, 125000008, 125000080, 125000800, 125008000, 125080000, 125800000, 128078125, 128781250, 133000000, 135812500, 156250064, 156250640, 156256400, 156314000, 156890000, 160000625, 160006250, 160062500, 160625000, 162650000, 166250000, 195313012, 195317620, 195363700, 195824500, 200000000, 200000005, 200000050, 200000500, 200005000, 200050000, 200056250, 200432500, 200500000, 205000000, 206125000, 220250000, 222500000, 244144721, 244181585, 244550225, 246512500, 248236625, 250000000, 250000004, 250000040, 250000400, 250004000, 250040000, 250400000, 253628125, 254000000, 256390625, 259906250, 285100625, 290000000, 295062500, 312500032, 312500320, 312503200, 312532000, 312820000, 315700000, 320003125, 320031250, 320312500, 323125000, 344500000, 351250000, 390625256, 390627560, 390650600, 390881000, 393185000, 400000025, 400000250, 400002500, 400025000, 400250000, 402500000, 416225000, 425000000, 488283298, 488301730, 488486050, 490329250, 500000002, 500000020, 500000200, 500002000, 500020000, 500200000, 502000000, 508761250, 513953125, 520000000, 531531250, 625000016, 625000160, 625001600, 625016000, 625160000, 626600000, 632500000, 640015625, 640156250, 641000000, 641562500, 646625000, 650000000, 653740625, 655625000, 693081250, 700000000, 707312500, 781250128, 781251280, 781262800, 781378000, 782530000, 785000000, 794050000, 796250000, 800000125, 800001250, 800012500, 800125000, 801250000, 812500000, 909250000, 925000000, 976563524, 976572740, 976664900, 977586500, 986802500, 1000000001, 1000000010, 1000000100, 1000001000, 1000010000, 1000100000, 1001000000, 1010000000, 1033765625, 1078962500, 1100000000, 1121656250, 1220711317, 1220785045, 1221522325, 1228895125, 1250000008, 1250000080, 1250000800, 1250008000, 1250080000, 1250800000, 1258000000, 1280078125, 1280781250, 1287812500, 1302623125, 1330000000, 1358125000, 1562500064, 1562500640, 1562506400, 1562564000, 1563140000, 1568900000, 1600000625, 1600006250, 1600062500, 1600625000, 1606250000, 1626500000, 1662500000, 1953125512, 1953130120, 1953176200, 1953637000, 1958245000, 2000000000, 2000000005, 2000000050, 2000000500, 2000005000, 2000050000, 2000500000, 2000562500, 2004325000, 2005000000, 2039903125, 2050000000, 2061250000, 2096828125, 2202500000, 2225000000, 2441410346, 2441447210, 2441815850, 2445502250, 2465125000, 2482366250, 2500000000, 2500000004, 2500000040, 2500000400, 2500004000, 2500040000, 2500400000, 2504000000, 2536281250, 2540000000, 2560390625, 2563906250, 2599062500, 2851006250.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 2271 values, from 2 to 986802500000000).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 2003 | 268 | 2 | ||||||||
| 3 | 0 | 1127 | 1144 | 3 | |||||||
| 4 | 1733 | 266 | 270 | 2 | 4 | ||||||
| 5 | 2091 | 50 | 48 | 39 | 43 | 5 | |||||
| 6 | 0 | 133 | 1009 | 0 | 994 | 135 | 6 | ||||
| 7 | 381 | 311 | 316 | 317 | 314 | 319 | 313 | 7 | |||
| 8 | 1473 | 133 | 266 | 1 | 260 | 133 | 4 | 1 | 8 | ||
| 9 | 0 | 0 | 1144 | 0 | 0 | 0 | 0 | 1127 | 0 | 9 | |
| 10 | 1858 | 19 | 42 | 5 | 38 | 233 | 31 | 6 | 34 | 5 | 10 |
| 11 | 229 | 228 | 128 | 240 | 431 | 0 | 0 | 465 | 215 | 110 | 225 |
A pictorial representation of the table above
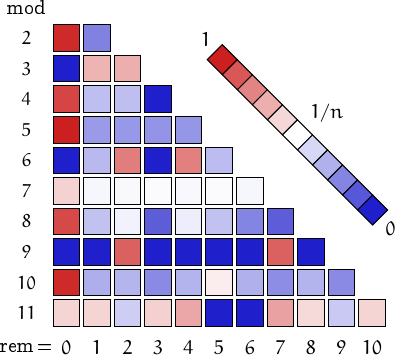
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits