• 4 can be written using four 4's:
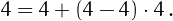
• 11 + 22 + 33 + 44 = 1! ⋅ 2! ⋅ 3! ⋅ 4!.
• Lagrange proved in 1770 that every natural number is the sum of at most 4 square numbers.
4 has 3 divisors (see below), whose sum is σ = 7. Its totient is φ = 2.
The previous prime is 3. The next prime is 5.
The square root of 4 is 2.
It is a perfect power (a square), and thus also a powerful number.
It is a Jordan-Polya number, since it can be written as (2!)2.
4 is nontrivially palindromic in base 3.
4 is an esthetic number in base 4, because in such base its adjacent digits differ by 1.
It is a semiprime because it is the product of two primes, and also a brilliant number, because the two primes have the same length.
It is an interprime number because it is at equal distance from previous prime (3) and next prime (5).
It is the 3-rd Motzkin number.
It is a trimorphic number since its cube, 64, ends in 4.
It is a Smith number, since the sum of its digits (4) coincides with the sum of the digits of its prime factors.
It is a Harshad number since it is a multiple of its sum of digits (4).
It is a super Niven number, because it is divisible the sum of any subset of its (nonzero) digits.
It is a nude number because it is divisible by every one of its digits and also a Zuckerman number because it is divisible by the product of its digits.
4 is an idoneal number.
It is a tribonacci number.
It is a tetranacci number.
It is a Lucas number.
It is an Ulam number.
It is (trivially) a d-powerful number and an alternating number.
It is a cake number, because a cake can be divided into 4 parts by 2 planar cuts.
It is a pancake number, because a pancake can be divided into 4 parts by 2 straight cuts.
It is one of the 548 Lynch-Bell numbers.
It is a compositorial, being equal to the product of composites up to 4.
It is a Duffinian number.
4 is a nontrivial repdigit in base 3.
It is a plaindrome in base 3.
It is a nialpdrome in base 2, base 3 and base 4.
It is a zygodrome in base 3.
It is a panconsummate number.
It is the 2-nd tetrahedral number.
A polygon with 4 sides can be constructed with ruler and compass.
It is an impolite number, since it cannot be written as a nontrivial sum of consecutive naturals.
It is equal to the Eulerian number A(3, 1).
It is a (trivial) narcissistic number.
4 is a highly composite number, because it has more divisors than any smaller number.
4 is a superabundant number, because it has a larger abundancy index than any smaller number.
4 is the 2-nd square number.
4 is the 2-nd centered triangular number.
It is a practical number, because each smaller number is the sum of distinct divisors of 4
4 is a deficient number, since it is larger than the sum of its proper divisors (3).
4 is a wasteful number, since it uses less digits than its factorization.
With its successor (5) it forms an eRAP, since the sums of their prime factors are consecutive (4 and 5).
With its predecessor (3) it forms an eRAP, since the sums of their prime factors are consecutive (3 and 4).
4 is an odious number, because the sum of its binary digits is odd.
The sum of its prime factors is 4 (or 2 counting only the distinct ones).
The product of its digits is 4, while the sum is 4.
The cubic root of 4 is about 1.5874010520.
The spelling of 4 in words is "four", and thus it is an aban number, an eban number, and an iban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.075 sec. • engine limits •

