• 11 can be written using four 4's:

• 112 = 121 is the smallest square that contains exactly two digits '1'.
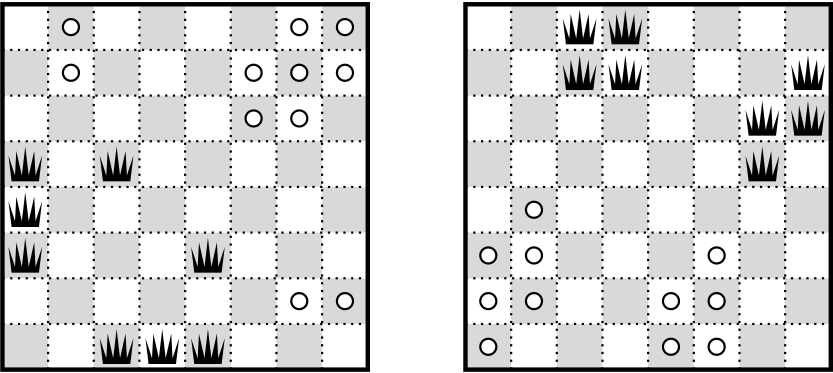
• When placing 8 queens on a 8×8 board, there can be at most 11 unattacked vacant squares. Two of the seven essentially distinct configurations:
11 has 2 divisors, whose sum is σ = 12. Its totient is φ = 10.
The previous prime is 7. The next prime is 13.
11 is nontrivially palindromic in base 10.
11 is digitally balanced in base 3, because in such base it contains all the possibile digits an equal number of times.
11 is an esthetic number in base 4, base 5, base 9 and base 11, because in such bases its adjacent digits differ by 1.
It is an a-pointer prime, because the next prime (13) can be obtained adding 11 to its sum of digits (2).
It is a strong prime.
It is a palprime.
It is a sliding number, since 11 = 1 + 10 and 1/1 + 1/10 = 1.1.
It is a cyclic number.
It is not a de Polignac number, because 11 - 22 = 7 is a prime.
It is a Sophie Germain prime.
Together with 13, it forms a pair of twin primes.
It is a Chen prime.
It is a nude number because it is divisible by every one of its digits and also a Zuckerman number because it is divisible by the product of its digits.
It is a Lucas number.
It is the 5-th Jacobsthal number.
It is a magnanimous number.
It is an Ulam number.
11 is a strobogrammatic number because it is the same when read upside-down.
It is a pancake number, because a pancake can be divided into 11 parts by 4 straight cuts.
11 is strictly pandigital in base 3.
It is a partition number, being equal to the number of ways a set of 6 identical objects can be partitioned into subset.
11 is a nontrivial repdigit in base 10.
It is a plaindrome in base 4, base 6, base 7, base 8, base 9 and base 10.
It is a nialpdrome in base 5, base 10 and base 11.
It is a zygodrome in base 10.
It is a panconsummate number.
It is a pernicious number, because its binary representation contains a prime number (3) of ones.
It is a good prime.
It is a polite number, since it can be written as a sum of consecutive naturals, namely, 5 + 6.
It is equal to the Eulerian number A(4, 1).
It is an arithmetic number, because the mean of its divisors is an integer number (6).
11 is the 2-nd centered decagonal number.
11 is a deficient number, since it is larger than the sum of its proper divisors (1).
11 is an equidigital number, since it uses as much as digits as its factorization.
11 is an odious number, because the sum of its binary digits is odd.
The product of its digits is 1, while the sum is 2.
The square root of 11 is about 3.3166247904. The cubic root of 11 is about 2.2239800906.
The spelling of 11 in words is "eleven", and thus it is an aban number, an iban number, an oban number, and an uban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.074 sec. • engine limits •

