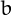plaindromes

A number is a plaindrome in a given base $b$

(often 10 or 16) if its digits are in nondecreasing order in that base.

For example, 1234, 2222, 25667 and 2468 are all plaindromes in base 10.

Clearly a plaindrome cannot contain the digit 0, unless it is the number 0 itself, so the plaindromes in base 2 correspond to numbers of the form 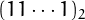$(11\cdots1)_2$ , i.e., to numbers of the form $2^k-1$ .

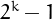A plaindrome in which the digits are strictly increasing is called metadrome, while numbers whose digits are nonincreasing and strictly decreasing are called nialpdromes and katadromes.

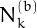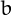The number $N^{(b)}_k$ of plaindromes of $k>1$ digits in base $b$ is equal to

$N^{(b)}_k = {{k+b-2}\choose {b-2}}\,,$

which, for $b=2$

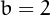collapses to 1, and for $b=3$

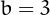simplifies to $k+1$

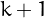. In general 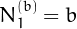$N^{(b)}_1=b$ , since we count also the 0 among the 1-digit plaindromes.

The total number 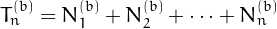$T^{(b)}_n = N^{(b)}_1+N^{(b)}_2+\cdots+N^{(b)}_n$ of plaindromes in base 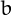$b$ with at most 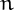$n$ digits is equal to

$T^{(b)}_n = {{n+b-1}\choose{b-1}}\,.$

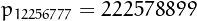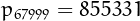Probably the largest plaindrome primes with index respectively plaindrome and nialdrome are $p_{12256777}=222578899$ and $p_{67999}=855331$ . See the nialpdromes for the symmetric pair.

The first plaindromes (in base 10) are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 16, 17, 18, 19, 22 more terms

Below, the spiral pattern of plaindromes in base 10 up to 4900. See the page on prime numbers for an explanation and links to similar pictures.

Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

A graph displaying how many plaindromes are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Useful links Mathworld, Plaindrome
OEIS, Sequence A009994 (base 10)
OEIS, Sequence A023757 (base 16)

Plaindromes can also be... (you may click on names or numbers and on + to get more values)

a-pointer 11 13 3469 + 5666677889 ABA 18 24 128 + 5555557777778 aban 11 12 13 + 999 abundant 12 18 24 + 48888888 Achilles 288 1125 1568 + 44677778888 admirable 12 24 56 + 55577788 alt.fact. 19 35899 alternating 12 14 16 + 123456789 amenable 12 13 16 + 888888889 amicable 122368 anti-perfect 244 apocalyptic 157 222 224 + 29999 arithmetic 11 13 14 + 9999999 astonishing 15 27 3388 automorphic 25 balanced p. 157 257 1123 + 6888899999 Bell 15 betrothed 48 binomial 15 28 35 + 3555557777778 brilliant 14 15 25 + 888888899 c.decagonal 11 c.heptagonal 22 148 2458 c.nonagonal 28 55 136 + 22222227777778 c.octagonal 25 49 169 + 277777788888889 c.pentagonal 16 226 456 + 444444455555556 c.square 13 25 113 + 22222224444445 c.triangular 19 46 136 + 1344555888889 cake 15 26 299 + 23479 Canada 125 16999 Carol 47 223 Catalan 14 Chen 11 13 17 + 88888999 compositorial 24 congruent 13 14 15 + 9999999 constructible 12 15 16 + 12336 cube 27 125 Cullen 25 Cunningham 15 17 24 + 899999999999999 Curzon 14 18 26 + 177777789 cyclic 11 13 15 + 8999999 D-number 15 33 39 + 6667779 d-powerful 24 89 135 + 6667789 de Polignac 127 149 337 + 88889999 decagonal 27 126 1117777 deceptive 259 3367 7777 + 11111111111 deficient 11 13 14 + 9999999 dig.balanced 11 12 15 + 188899999 double fact. 15 48 Duffinian 16 25 27 + 8999999 eban 34 36 44 + 66 economical 11 13 14 + 19999999 emirp 13 17 37 + 177777799 emirpimes 15 26 39 + 79999999 enlightened 256 equidigital 11 13 14 + 19999999 eRAP 24 2255 12568899 1222337999 esthetic 12 23 34 + 123456789 Eulerian 11 26 57 + 247 evil 12 15 17 + 889999999 factorial 24 fibodiv 14 19 28 + 1999999999 Fibonacci 13 34 55 + 377 Friedman 25 125 126 + 455679 frugal 125 128 256 + 555588999 gapful 135 225 1111 + 77788888999 Gilda 29 49 78 good prime 11 17 29 + 133333777 happy 13 19 23 + 7788999 harmonic 28 Harshad 12 18 24 + 8888888889 heptagonal 18 34 55 + 444444468888889 hex 19 37 127 + 133333366666669 hexagonal 15 28 45 + 355555577777778 highly composite 12 24 36 48 hoax 22 58 136 + 66677788 Hogben 13 57 111 + 44444455555557 Honaker 457 3559 12277 + 345555569 house 78 155 2234 35555 hungry 17 144 hyperperfect 28 1333 iban 11 12 14 + 777777 iccanobiF 13 39 124 idoneal 12 13 15 + 357 impolite 16 128 256 inconsummate 266 377 466 + 689999 insolite 111 11112 111111111 interprime 12 15 18 + 77778888 Jacobsthal 11 Jordan-Polya 12 16 24 + 12288 junction 111 113 115 + 33333334 Kaprekar 45 55 99 + 999999999999999 Kynea 23 79 Lehmer 15 133 247 + 2478889999 Leyland 17 57 145 + 1124 lonely 23 1344 Lucas 11 18 29 + 5778 lucky 13 15 25 + 8899999 Lynch-Bell 12 15 24 + 1368 m-pointer 23 1123 magic 15 34 111 + 23346 magnanimous 11 12 14 + 222245 metadrome 12 13 14 + 123456789 modest 13 19 23 + 1999999999 Moran 18 27 45 + 56666699 Motzkin 127 2356779 nialpdrome 11 22 33 + 999999999999999 nonagonal 24 46 111 + 223399 nude 11 12 15 + 488888888 O'Halloran 12 36 44 + 156 oban 11 12 13 + 999 octagonal 133 225 13333 + 133333333333333 odious 11 13 14 + 999999999 Ormiston 122579 123379 355679 + 1566677779 palindromic 11 22 33 + 999999999999999 palprime 11 pancake 11 16 22 + 355555577777779 panconsummate 11 12 14 + 337 pandigital 11 15 19 + 334466788 partition 11 15 22 + 1255 pentagonal 12 22 35 + 13444557 perfect 28 pernicious 11 12 13 + 8889999 Perrin 12 17 22 + 367 Pierpont 13 17 19 + 12289 Poulet 23377 223345 256999 1333333 power 16 25 27 + 44444448888889 powerful 16 25 27 + 277777788888889 practical 12 16 18 + 6678888 prim.abundant 12 18 56 + 55577788 prime 11 13 17 + 788888888899 primeval 13 37 113 + 1123456789 productive 12 16 22 + 11578 pronic 12 56 156 + 44444455555556 Proth 13 17 25 + 1124466689 pseudoperfect 12 18 24 + 999999 repdigit 11 22 33 + 999999999999999 repfigit 14 19 28 + 4788 repunit 13 15 57 + 111111111111111 Rhonda 1568 245579 2258999 Ruth-Aaron 15 16 24 + 115555777 self 222 233 244 + 888888999 self-describing 22 4444 224444 + 66666688888888 semiprime 14 15 22 + 88899999 sliding 11 25 29 + 15689 Smith 22 27 58 + 66666668 Sophie Germain 11 23 29 + 7777778999 sphenic 66 78 114 + 88999999 square 16 25 36 + 277777788888889 star 13 37 337 + 1122337 straight-line 111 123 135 + 999999999999999 strobogrammatic 11 69 88 + 888888888888888 strong prime 11 17 29 + 68888999 subfactorial 44 super Niven 12 24 36 48 super-d 19 69 119 + 7778899 superabundant 12 24 36 48 tau 12 18 24 + 777788888 tetrahedral 35 56 455 tetranacci 15 29 56 triangular 15 28 36 + 355555577777778 tribonacci 13 24 44 149 trimorphic 24 25 49 + 999999999999999 truncatable prime 13 17 23 + 233347 twin 11 13 17 + 677888999 uban 11 12 13 + 99 Ulam 11 13 16 + 9999999 unprimeable 1134 1135 1136 + 8888888 untouchable 88 124 146 + 788888 upside-down 19 28 37 + 555555555555555 wasteful 12 18 22 + 9999999 weak prime 13 19 23 + 89999999 Woodall 17 23 159 + 129999999999999 Zeisel 233569 Zuckerman 11 12 15 + 1111144448 Zumkeller 12 24 28 + 78888 zygodrome 11 22 33 + 999999999999999