• 5 can be written using four 4's:
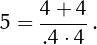
• If 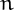 2 + 1 and (
2 + 1 and (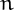 +1)2 + 1 are both divisible by a number
+1)2 + 1 are both divisible by a number 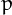 > 1, then
> 1, then 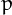 = 5. (For example, this happens for
= 5. (For example, this happens for 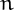 = 7.)
= 7.)
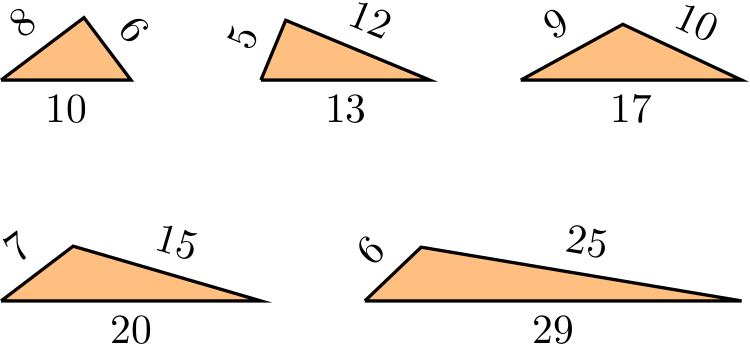
• Among triangles with integer sides, there are only 5
5 has 2 divisors, whose sum is σ = 6. Its totient is φ = 4.
The previous prime is 3. The next prime is 7.
It is the 5-th Fibonacci number F5.
It is an alternating factorial (5 = 3! - 2! + 1!).
5 is nontrivially palindromic in base 2 and base 4.
It is a Cunningham number, because it is equal to 22+1.
5 is an esthetic number in base 2, base 3 and base 5, because in such bases its adjacent digits differ by 1.
It is a balanced prime because it is at equal distance from previous prime (3) and next prime (7).
It can be written as a sum of positive squares in only one way, i.e., 4 + 1 = 2^2 + 1^2 .
Together with 1645333507 or 188748146801, it forms a Wieferich pair.
It is a cyclic number.
It is the 3-rd Bell number.
It is the 3-rd Catalan number.
It is an automorphic number since its square, 25, ends in 5.
It is a trimorphic number since its cube, 125, ends in 5.
It is not a de Polignac number, because 5 - 21 = 3 is a prime.
It is a Sophie Germain prime.
Together with 7, it forms a pair of twin primes.
It is a Chen prime.
It is a Harshad number since it is a multiple of its sum of digits (5).
It is a super Niven number, because it is divisible the sum of any subset of its (nonzero) digits.
It is a nude number because it is divisible by every one of its digits and also a Zuckerman number because it is divisible by the product of its digits.
It is an iccanobiF number.
5 is an idoneal number.
It is the 4-th Jacobsthal number.
It is (trivially) a d-powerful number and an alternating number.
It is one of the 548 Lynch-Bell numbers.
It is a hungry number.
5 is an undulating number in base 2.
It is the 5-th Perrin number.
It is a Curzon number.
It is a partition number, being equal to the number of ways a set of 4 identical objects can be partitioned into subset.
5 is a nontrivial repdigit in base 4.
It is a plaindrome in base 3 and base 4.
It is a nialpdrome in base 4 and base 5.
It is a zygodrome in base 4.
It is a self number, because there is not a number n which added to its sum of digits gives 5.
It is a congruent number.
It is a panconsummate number.
5 is an untouchable number, because it is not equal to the sum of proper divisors of any number.
It is a pernicious number, because its binary representation contains a prime number (2) of ones.
It is an upside-down number.
It is a good prime.
It is a Pierpont prime, being equal to 22 ⋅ 30 + 1.
A polygon with 5 sides can be constructed with ruler and compass.
It is a polite number, since it can be written as a sum of consecutive naturals, namely, 2 + 3.
It is an arithmetic number, because the mean of its divisors is an integer number (3).
It is the magic constant of a 2 × 2 magic square, which unfortunately does not exist...
It is a (trivial) narcissistic number.
It is a Proth number, since it is equal to 1 ⋅ 22 + 1 and 1 < 22.
5 is the 2-nd pentagonal number.
5 is the 2-nd centered square number.
It is an amenable number.
5 is a deficient number, since it is larger than the sum of its proper divisors (1).
5 is an equidigital number, since it uses as much as digits as its factorization.
With its successor (6) it forms a Ruth-Aaron pair, since the sum of their distinct prime factors is the same (5).
With its predecessor (4) it forms an eRAP, since the sums of their prime factors are consecutive (4 and 5).
5 is an evil number, because the sum of its binary digits is even.
The product of its digits is 5, while the sum is 5.
The square root of 5 is about 2.2360679775. The cubic root of 5 is about 1.7099759467.
The spelling of 5 in words is "five", and thus it is an aban number, an oban number, and an uban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.069 sec. • engine limits •

