• 97 can be written using four 4's:

• Probably every number ≥ 97 can be written as the sum of distinct primes with prime indexes. For example, 97 = p(p(1)) + p(p(3)) + p(p(9)).
• Using all the digits from 0 to 9 once, it is possible to write 97 pairs of fractions such that each pair sums to 1. For example, 79/83 + 60/1245 = 98/136 + 57/204 = 1/2 + 4538/9076 = 1.
• Sorting the digits of 297 in ascending order we obtain a prime of 26 digits.
•
Probably 97 is the only 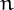 > 2 such that
> 2 such that  ! contains all its
prime factors as substrings.
! contains all its
prime factors as substrings.
97 has 2 divisors, whose sum is σ = 98. Its totient is φ = 96.
The previous prime is 89. The next prime is 101. The reversal of 97 is 79.
It is a happy number.
97 is nontrivially palindromic in base 8.
97 is an esthetic number in base 3, base 11, base 13 and base 15, because in such bases its adjacent digits differ by 1.
It is a strong prime.
It can be written as a sum of positive squares in only one way, i.e., 81 + 16 = 9^2 + 4^2 .
97 is a truncatable prime.
It is an emirp because it is prime and its reverse (79) is a distict prime.
It is a cyclic number.
It is not a de Polignac number, because 97 - 23 = 89 is a prime.
It is an Ulam number.
97 is an undulating number in base 8.
It is a plaindrome in base 7, base 9, base 11, base 14 and base 15.
It is a nialpdrome in base 10, base 12, base 13 and base 16.
It is a self number, because there is not a number n which added to its sum of digits gives 97.
It is a pernicious number, because its binary representation contains a prime number (3) of ones.
It is a good prime.
It is a Pierpont prime, being equal to 25 ⋅ 31 + 1.
It is a polite number, since it can be written as a sum of consecutive naturals, namely, 48 + 49.
It is an arithmetic number, because the mean of its divisors is an integer number (49).
It is a Proth number, since it is equal to 3 ⋅ 25 + 1 and 3 < 25.
It is an amenable number.
97 is a deficient number, since it is larger than the sum of its proper divisors (1).
97 is an equidigital number, since it uses as much as digits as its factorization.
97 is an odious number, because the sum of its binary digits is odd.
The product of its digits is 63, while the sum is 16.
The square root of 97 is about 9.8488578018. The cubic root of 97 is about 4.5947008922.
Subtracting from 97 its sum of digits (16), we obtain a 4-th power (81 = 34).
The spelling of 97 in words is "ninety-seven", and thus it is an aban number, an oban number, and an uban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.034 sec. • engine limits •

