 , for
, for 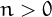 , which
gives the sum of the squares of the digits of
, which
gives the sum of the squares of the digits of 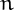 ,
so, for example,
,
so, for example, 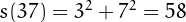 .
.
If we start from a number 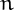 and we repeatedly apply
and we repeatedly apply 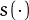 , we
obtain a sequence
, we
obtain a sequence 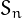 of numbers
of numbers 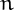 ,
, 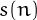 ,
, 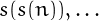 , and so on.
, and so on.
A number 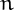 is called happy if
is called happy if 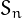 contains the number 1.
contains the number 1.
Note that 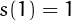 , so in that case the sequence
, so in that case the sequence 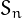 has an infinite
tail of
has an infinite
tail of  's.
's.
If a number is not happy then it is easy to see
that at a certain point 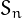 will enter the infinite loop
will enter the infinite loop
![\[\dots,4, 16, 37, 58, 89, 145, 42, 20, 4,\dots\]](pic.10.png)
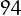 we obtain
we obtain
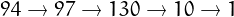 ,
so
,
so 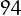 is happy. See figure aside.
is happy. See figure aside.
On the contrary, starting from
61 we obtain 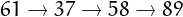 and thus 61 is not
happy, since 89 belongs to the unhappy loop.
and thus 61 is not
happy, since 89 belongs to the unhappy loop.
The first 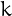 -tuple of consecutive happy numbers,
for
-tuple of consecutive happy numbers,
for 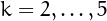 starts at 31, 1880, 7839, and 44488, respectively.
starts at 31, 1880, 7839, and 44488, respectively.
E. El-Sedy & S. Siksek proved that there can be runs of arbitrary length.
There are 3, 20, 143, 1442, 14377, 143071,... happy numbers up to 10, 100, 1000,....
The smallest 3 × 3 magic square whose entries are happy numbers is
| 907 | 1188 | 635 |
| 638 | 910 | 1182 |
| 1185 | 632 | 913 |
The first happy numbers are 1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79, 82, 86, 91, 94, 97, 100, 103, 109, 129, 130 more terms