• 63 can be written using four 4's:
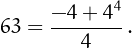
• 632 = 3969 is the smallest square that contains exactly two digits '9'.
63 has 6 divisors (see below), whose sum is σ = 104. Its totient is φ = 36.
The previous prime is 61. The next prime is 67. The reversal of 63 is 36.
63 is nontrivially palindromic in base 2, base 4 and base 8.
It is a Cunningham number, because it is equal to 26-1.
63 is an esthetic number in base 15, because in such base its adjacent digits differ by 1.
It is not a de Polignac number, because 63 - 21 = 61 is a prime.
It is a Harshad number since it is a multiple of its sum of digits (9), and also a Moran number because the ratio is a prime number: 7 = 63 / (6 + 3).
It is a d-powerful number, because it can be written as 33 + 62 .
It is a D-number.
It is an alternating number because its digits alternate between even and odd.
It is a Duffinian number.
63 is a lucky number.
63 is a nontrivial repdigit in base 2, base 4 and base 8.
It is a plaindrome in base 2, base 4, base 5, base 8, base 11, base 13, base 14 and base 16.
It is a nialpdrome in base 2, base 3, base 4, base 8, base 9, base 10, base 12 and base 15.
It is a zygodrome in base 2, base 4 and base 8.
It is a congruent number.
It is an inconsummate number, since it does not exist a number n which divided by its sum of digits gives 63.
Being equal to 4×24-1, it is a Woodall number.
It is a nontrivial repunit in base 2.
It is a polite number, since it can be written in 5 ways as a sum of consecutive naturals, for example, 6 + ... + 12.
63 is a deficient number, since it is larger than the sum of its proper divisors (41).
63 is a wasteful number, since it uses less digits than its factorization.
63 is an evil number, because the sum of its binary digits is even.
The sum of its prime factors is 13 (or 10 counting only the distinct ones).
The product of its digits is 18, while the sum is 9.
The square root of 63 is about 7.9372539332. The cubic root of 63 is about 3.9790572079.
Adding to 63 its product of digits (18), we get a 4-th power (81 = 34).
Subtracting from 63 its product of digits (18), we obtain a triangular number (45 = T9).
Adding to 63 its reverse (36), we get a palindrome (99).
Subtracting from 63 its reverse (36), we obtain a cube (27 = 33).
The spelling of 63 in words is "sixty-three", and thus it is an aban number, an oban number, and an uban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.071 sec. • engine limits •

