• 13 can be written using four 4's:
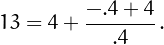
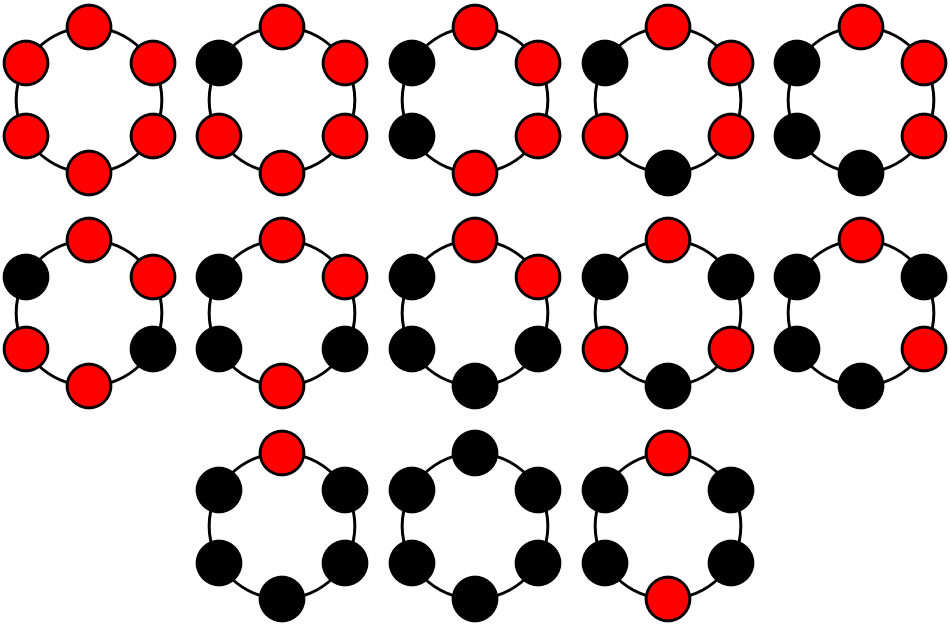
• There are 13 essentially distinct necklaces that can be made with 6 beads and two available colors:
• 13 is the 6-th prime and 6 = 1! ⋅ 3!. The next such prime is 226130351.
• If  2 + 3 and (
2 + 3 and ( +1)2 + 3 are both divisible by a number
+1)2 + 3 are both divisible by a number 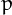 > 1, then
> 1, then 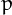 = 13. (For example, this happens for
= 13. (For example, this happens for 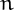 = 6.)
= 6.)
• 132 = 169 is an anagram of the next square 142 = 196.
• 13 is the smallest k such that the even and the odd digits of 2k (here 8192) have the same sum, 8 + 2 = 1 + 9. The largest such k is probably 386.
13 has 2 divisors, whose sum is σ = 14. Its totient is φ = 12.
The previous prime is 11. The next prime is 17. The reversal of 13 is 31.
It is a happy number.
It is the 7-th Fibonacci number F7.
13 is nontrivially palindromic in base 3 and base 12.
It is the 2-nd star number.
13 is an esthetic number in base 5, base 6, base 11 and base 13, because in such bases its adjacent digits differ by 1.
It is an a-pointer prime, because the next prime (17) can be obtained adding 13 to its sum of digits (4).
It is a weak prime.
It can be written as a sum of positive squares in only one way, i.e., 9 + 4 = 3^2 + 2^2 .
13 is a truncatable prime.
It is an emirp because it is prime and its reverse (31) is a distict prime.
It is a cyclic number.
It is not a de Polignac number, because 13 - 21 = 11 is a prime.
Together with 11, it forms a pair of twin primes.
It is a Chen prime.
It is an iccanobiF number.
13 is an idoneal number.
It is a tribonacci number.
It is an Ulam number.
It is the 4-th Hogben number.
13 is a modest number, since divided by 3 gives 1 as remainder.
It is the 3-rd primeval number, because it sets a new record (3) in the number of distinct primes that is it possible to write using its digits.
13 is a lucky number.
13 is a nontrivial repdigit in base 3 and base 12.
It is a plaindrome in base 3, base 5, base 7, base 8, base 9, base 10, base 11 and base 12.
It is a nialpdrome in base 3, base 4, base 6, base 12 and base 13.
It is a zygodrome in base 3 and base 12.
It is a congruent number.
It is a nontrivial repunit in base 3.
It is a pernicious number, because its binary representation contains a prime number (3) of ones.
It is a Pierpont prime, being equal to 22 ⋅ 31 + 1.
It is a polite number, since it can be written as a sum of consecutive naturals, namely, 6 + 7.
It is an arithmetic number, because the mean of its divisors is an integer number (7).
It is a Proth number, since it is equal to 3 ⋅ 22 + 1 and 3 < 22.
13 is the 3-rd centered square number.
It is an amenable number.
13 is a deficient number, since it is larger than the sum of its proper divisors (1).
13 is an equidigital number, since it uses as much as digits as its factorization.
It is an anagram of its base 4 representation: 13 = (31)4.
13 is an odious number, because the sum of its binary digits is odd.
The product of its digits is 3, while the sum is 4.
The square root of 13 is about 3.6055512755. The cubic root of 13 is about 2.3513346877.
Adding to 13 its reverse (31), we get a palindrome (44).
The spelling of 13 in words is "thirteen", and thus it is an aban number, an oban number, and an uban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.076 sec. • engine limits •

