• 8 can be written using four 4's:
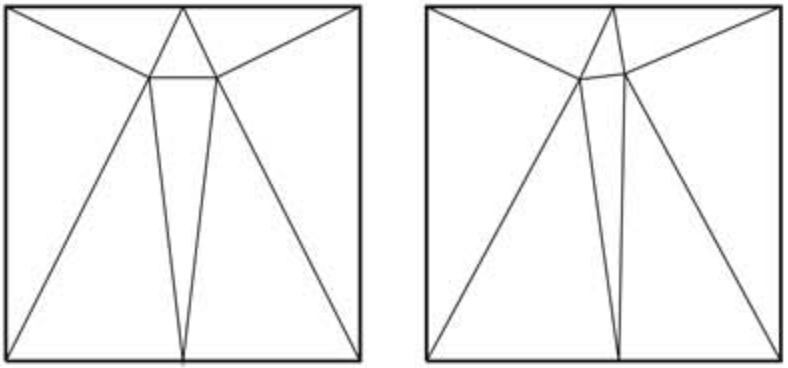
• A dissection of a square into acute triangles contains at least 8 triangles:
8 has 4 divisors (see below), whose sum is σ = 15. Its totient is φ = 4.
The previous prime is 7. The next prime is 11.
The cubic root of 8 is 2.
It is a perfect power (a cube), and thus also a powerful number.
It is the 6-th Fibonacci number F6.
It is a Jordan-Polya number, since it can be written as (2!)3.
It is a double factorial (8 = 4 !! = 2 ⋅ 4 ).
8 is nontrivially palindromic in base 3 and base 7.
It is a Cunningham number, because it is equal to 32-1.
8 is an esthetic number in base 6 and base 8, because in such bases its adjacent digits differ by 1.
It can be written as a sum of positive squares in only one way, i.e., 4 + 4 = 2^2 + 2^2 .
It is a tau number, because it is divible by the number of its divisors (4).
It is an ABA number since it can be written as A⋅BA, here for A=2, B=2.
It is a Harshad number since it is a multiple of its sum of digits (8).
It is a super Niven number, because it is divisible the sum of any subset of its (nonzero) digits.
It is a Leyland number of the form 22 + 22.
It is a nude number because it is divisible by every one of its digits and also a Zuckerman number because it is divisible by the product of its digits.
It is an iccanobiF number.
8 is an idoneal number.
It is a tetranacci number.
It is an Ulam number.
It is (trivially) a d-powerful number and an alternating number.
8 is a strobogrammatic number because it is the same when read upside-down.
It is a cake number, because a cake can be divided into 8 parts by 3 planar cuts.
It is one of the 548 Lynch-Bell numbers.
It is a O'Halloran number.
It is a Duffinian number.
8 is a nontrivial repdigit in base 3 and base 7.
It is a plaindrome in base 3, base 5, base 6 and base 7.
It is a nialpdrome in base 2, base 3, base 4, base 7 and base 8.
It is a zygodrome in base 3 and base 7.
It is a panconsummate number.
A polygon with 8 sides can be constructed with ruler and compass.
It is an impolite number, since it cannot be written as a nontrivial sum of consecutive naturals.
It is a (trivial) narcissistic number.
8 is the 2-nd octagonal number.
8 is the 2-nd centered heptagonal number.
It is an amenable number.
It is a practical number, because each smaller number is the sum of distinct divisors of 8
8 is a deficient number, since it is larger than the sum of its proper divisors (7).
8 is a wasteful number, since it uses less digits than its factorization.
With its successor (9) it forms a Ruth-Aaron pair, since the sum of their prime factors is the same (6).
8 is an odious number, because the sum of its binary digits is odd.
The sum of its prime factors is 6 (or 2 counting only the distinct ones).
The product of its digits is 8, while the sum is 8.
The square root of 8 is about 2.8284271247.
The spelling of 8 in words is "eight", and thus it is an aban number, an oban number, and an uban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.072 sec. • engine limits •

