 a tau number if
a tau number if
 is divisible by the number
is divisible by the number 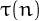 of its divisors, and
they proved that the natural density of tau numbers is zero.
of its divisors, and
they proved that the natural density of tau numbers is zero.
Later, S.Colton, by means of his automatic concept formation program HR, re-discovered them and called these numbers refactorable.
S.Colton proved that there are infinite tau numbers, since for every prime 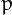 the number
the number 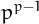 is refactorable and that
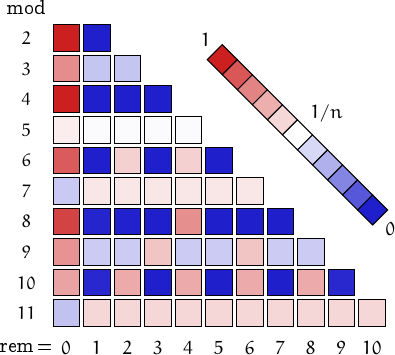
all the odd tau numbers are squares and that tau numbers
are congruent to 0, 1, 2 or 4
is refactorable and that
all the odd tau numbers are squares and that tau numbers
are congruent to 0, 1, 2 or 4 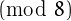 .
.
Moreover, Colton proved that, if 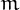 is the product of
is the product of 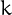 distinct primes, then there are
distinct primes, then there are 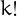 tau numbers with
tau numbers with 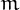 divisors.
For example, the tau numbers with
divisors.
For example, the tau numbers with 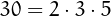 divisors are 720, 1200, 1620, 4050, 7500 and 11250.
divisors are 720, 1200, 1620, 4050, 7500 and 11250.
It is easy to see that, if 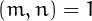 and
and 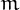 and
and 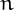 are
tau numbers, then
are
tau numbers, then 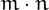 is also a tau number.
is also a tau number.
J.Zelinsky proved in 2002 that there are no 3 consecutive tau numbers. However, it is conjectured that there are infinite pairs of consecutive tau numbers, which, as Colton proved, always contain a square. The first ones are (1, 2), (8, 9), (1520, 1521) and (50624, 50625).
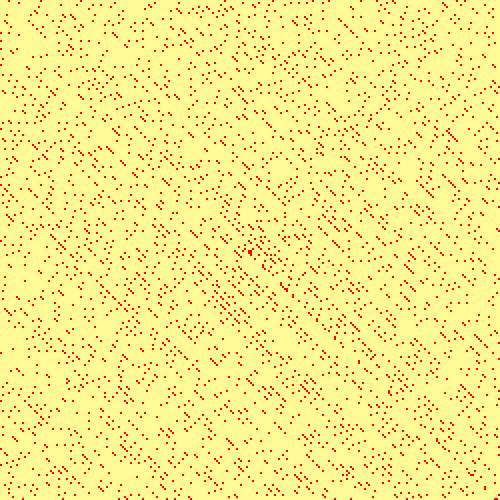
Below, the spiral pattern of tau numbers up to 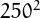 . See the page on prime numbers for an explanation and links to similar pictures.
. See the page on prime numbers for an explanation and links to similar pictures.
The smallest Pythagorean triple of tau numbers is (40, 96, 104). Is there a primitive such triple?
The first tau numbers are 1, 2, 8, 9, 12, 18, 24, 36, 40, 56, 60, 72, 80, 84, 88, 96, 104, 108, 128, 132, 136, 152, 156, 180, 184, 204, 225 more terms