• 269 can be written using four 4's:
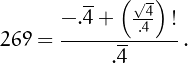
269 has 2 divisors, whose sum is σ = 270. Its totient is φ = 268.
The previous prime is 263. The next prime is 271. The reversal of 269 is 962.
It is a strong prime.
It can be written as a sum of positive squares in only one way, i.e., 169 + 100 = 13^2 + 10^2 .
It is a cyclic number.
It is not a de Polignac number, because 269 - 28 = 13 is a prime.
It is a super-2 number, since 2×2692 = 144722, which contains 22 as substring.
Together with 271, it forms a pair of twin primes.
It is a Chen prime.
It is a plaindrome in base 6, base 10, base 11, base 13 and base 15.
It is a nialpdrome in base 7.
It is a congruent number.
It is not a weakly prime, because it can be changed into another prime (263) by changing a digit.
It is a good prime.
It is a polite number, since it can be written as a sum of consecutive naturals, namely, 134 + 135.
It is an arithmetic number, because the mean of its divisors is an integer number (135).
It is an amenable number.
269 is a deficient number, since it is larger than the sum of its proper divisors (1).
269 is an equidigital number, since it uses as much as digits as its factorization.
269 is an evil number, because the sum of its binary digits is even.
The product of its digits is 108, while the sum is 17.
The square root of 269 is about 16.4012194669. The cubic root of 269 is about 6.4553148109.
Subtracting from 269 its sum of digits (17), we obtain a palindrome (252).
Subtracting from 269 its product of digits (108), we obtain a palindrome (161).
The spelling of 269 in words is "two hundred sixty-nine", and thus it is an aban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 1.024 sec. • engine limits •

