Search a number
twin primes
Two primes are said to be twins if their difference is 2, like in the pairs (29, 31) or (977779797977, 977779797979).

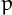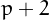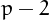So, a prime  $p$  is called twin prime if  $p+2$  or  $p-2$  is prime as well.

It is conjectured, but still not proved, that there are infinite twin primes.

Primes which do not belong to a twin pair are sometimes called isolated.

Probably all the even numbers greater than 4208 can be written as the sum of two twin primes.

The first twin pairs are (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109) more terms

Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
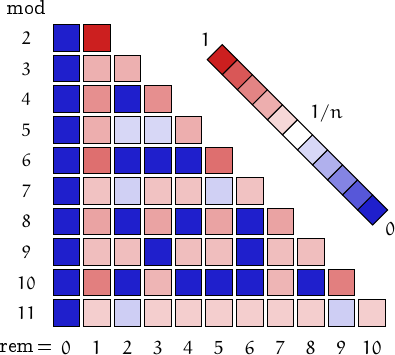
remainders of twin primes
Useful links Mathworld, Twin Primes
Wikipedia, Twin prime
OEIS, sequence A001097
Twin primes can also be... (you may click on names or numbers and on + to get more values)

a-pointer 11 13 101 103 + 999905971 aban 11 13 17 19 + 999000493 alt.fact. 19 101 619 4421 35899 alternating 29 41 43 61 + 989894749 amenable 13 17 29 41 + 999999193 apocalyptic 823 857 859 1019 + 29881 arithmetic 11 13 17 19 + 9999973 bemirp 1061 1091 10091 106861 + 199680881 c.decagonal 11 31 61 101 + 999768701 c.heptagonal 43 71 197 463 + 990252271 c.pentagonal 31 181 601 1051 + 995654731 c.square 13 41 61 181 + 999983921 c.triangular 19 31 109 199 + 998730919 canyon 101 103 107 109 + 987654379 Chen 11 13 17 19 + 99999587 congruent 13 29 31 41 + 9999973 constructible 17 65537 Cunningham 17 31 101 197 + 995402501 Curzon 29 41 281 641 + 199982969 cyclic 11 13 17 19 + 9999973 d-powerful 43 283 463 2083 + 9972583 de Polignac 149 599 809 1019 + 99996131 deficient 11 13 17 19 + 9999973 dig.balanced 11 19 41 139 + 199994369 economical 11 13 17 19 + 19999549 emirp 13 17 31 71 + 199999309 equidigital 11 13 17 19 + 19999549 esthetic 43 101 32321 32323 + 345434567 Eulerian 11 65519 478271 evil 17 29 43 71 + 999999193 fibodiv 19 61 149 199 + 2087 Fibonacci 13 Friedman 347 12107 12109 15641 + 995341 Gilda 29 good prime 11 17 29 41 + 199968539 happy 13 19 31 103 + 9999929 hex 19 61 271 1951 + 995304031 Hogben 13 31 43 73 + 998907631 Honaker 1049 1091 1301 1933 + 999815041 house 271 hungry 17 iban 11 17 41 43 + 777421 iccanobiF 13 idoneal 13 inconsummate 431 461 521 821 + 999331 Jacobsthal 11 43 2731 174763 715827883 junction 101 103 107 109 + 99999259 katadrome 31 41 43 61 + 98764321 Leyland 17 Lucas 11 29 199 521 lucky 13 31 43 73 + 9999049 m-pointer 61 1231 1321 2111 + 311221111 magnanimous 11 29 41 43 + 228440489 metadrome 13 17 19 29 + 1245689 modest 13 19 29 59 + 999311111 mountain 151 181 191 193 + 789865421 nialpdrome 11 31 41 43 + 999998641 nude 11 oban 11 13 17 19 + 883 odious 11 13 19 31 + 999999191 Ormiston 1931 25031 35897 37813 + 999980897 palindromic 11 101 151 181 + 999454999 palprime 11 101 151 181 + 999454999 pancake 11 29 137 191 + 998709779 panconsummate 11 31 43 59 + 1291 pandigital 11 19 partition 11 101 pernicious 11 13 17 19 + 9999973 Perrin 17 29 Pierpont 13 17 19 73 + 169869313 plaindrome 11 13 17 19 + 677888999 prime 11 13 17 19 + 999999193 primeval 13 107 137 10139 + 10034579 Proth 13 17 41 193 + 995622913 repdigit 11 repfigit 19 61 197 repunit 13 31 43 73 + 998907631 self 31 569 659 883 + 999996071 self-describing 10153331 16331531 17143331 19123331 + 33151931 sliding 11 29 101 641 Sophie Germain 11 29 41 179 + 999999191 star 13 73 181 433 + 972241021 straight-line 76543 strobogrammatic 11 101 181 619 + 690181069 strong prime 11 17 29 41 + 99999587 super-d 19 31 107 181 + 9999931 tetranacci 29 tribonacci 13 149 trimorphic 31249 281249 truncatable prime 13 17 29 31 + 998966653 uban 11 13 17 19 + 97000021 Ulam 11 13 197 241 + 9999161 undulating 101 151 181 191 + 1212121 upside-down 19 73 1289 3467 + 99955111 weak prime 13 19 31 43 + 99999589 weakly prime 294001 1062599 1524181 5575259 + 998839951 Wieferich 1093 Woodall 17 191 3124999 Zuckerman 11 zygodrome 11 11777 22111 22277 + 999922211