The first 600 nontrivial binomial coefficients :
6, 10, 15, 20, 21, 28, 35, 36, 45, 55, 56, 66, 70, 78, 84, 91, 105, 120, 126, 136, 153, 165, 171, 190, 210, 220, 231, 252, 253, 276, 286, 300, 325, 330, 351, 364, 378, 406, 435, 455, 462, 465, 495, 496, 528, 560, 561, 595, 630, 666, 680, 703, 715, 741, 780, 792, 816, 820, 861, 903, 924, 946, 969, 990, 1001, 1035, 1081, 1128, 1140, 1176, 1225, 1275, 1287, 1326, 1330, 1365, 1378, 1431, 1485, 1540, 1596, 1653, 1711, 1716, 1770, 1771, 1820, 1830, 1891, 1953, 2002, 2016, 2024, 2080, 2145, 2211, 2278, 2300, 2346, 2380, 2415, 2485, 2556, 2600, 2628, 2701, 2775, 2850, 2925, 2926, 3003, 3060, 3081, 3160, 3240, 3276, 3321, 3403, 3432, 3486, 3570, 3654, 3655, 3741, 3828, 3876, 3916, 4005, 4060, 4095, 4186, 4278, 4368, 4371, 4465, 4495, 4560, 4656, 4753, 4845, 4851, 4950, 4960, 5005, 5050, 5151, 5253, 5356, 5456, 5460, 5565, 5671, 5778, 5886, 5984, 5985, 5995, 6105, 6188, 6216, 6328, 6435, 6441, 6545, 6555, 6670, 6786, 6903, 7021, 7140, 7260, 7315, 7381, 7503, 7626, 7750, 7770, 7875, 8001, 8008, 8128, 8256, 8385, 8436, 8515, 8568, 8646, 8778, 8855, 8911, 9045, 9139, 9180, 9316, 9453, 9591, 9730, 9870, 9880, 10011, 10153, 10296, 10440, 10585, 10626, 10660, 10731, 10878, 11026, 11175, 11325, 11440, 11476, 11480, 11628, 11781, 11935, 12090, 12246, 12341, 12376, 12403, 12561, 12650, 12720, 12870, 12880, 13041, 13203, 13244, 13366, 13530, 13695, 13861, 14028, 14190, 14196, 14365, 14535, 14706, 14878, 14950, 15051, 15180, 15225, 15400, 15504, 15576, 15753, 15931, 16110, 16215, 16290, 16471, 16653, 16836, 17020, 17205, 17296, 17391, 17550, 17578, 17766, 17955, 18145, 18336, 18424, 18528, 18564, 18721, 18915, 19110, 19306, 19448, 19503, 19600, 19701, 19900, 20100, 20301, 20349, 20475, 20503, 20706, 20825, 20910, 21115, 21321, 21528, 21736, 21945, 22100, 22155, 22366, 22578, 22791, 23005, 23220, 23426, 23436, 23653, 23751, 23871, 24090, 24310, 24531, 24753, 24804, 24976, 25200, 25425, 25651, 25878, 26106, 26235, 26334, 26335, 26565, 26796, 27028, 27132, 27261, 27405, 27495, 27720, 27730, 27966, 28203, 28441, 28680, 28920, 29161, 29260, 29403, 29646, 29890, 30135, 30381, 30628, 30856, 30876, 31125, 31375, 31465, 31626, 31824, 31878, 32131, 32385, 32509, 32640, 32896, 33153, 33411, 33649, 33670, 33930, 34191, 34220, 34453, 34716, 34980, 35245, 35511, 35778, 35960, 35990, 36046, 36315, 36585, 36856, 37128, 37401, 37675, 37820, 37950, 38226, 38503, 38760, 38781, 39060, 39340, 39621, 39711, 39903, 40186, 40470, 40755, 40920, 41041, 41328, 41616, 41664, 41905, 42195, 42486, 42504, 42778, 43071, 43365, 43660, 43680, 43758, 43956, 44253, 44551, 44850, 45150, 45451, 45753, 45760, 46056, 46360, 46376, 46665, 46971, 47278, 47586, 47895, 47905, 48205, 48516, 48620, 48828, 49141, 49455, 49770, 50086, 50116, 50388, 50403, 50721, 51040, 51360, 51681, 52003, 52326, 52360, 52394, 52650, 52975, 53130, 53301, 53628, 53956, 54264, 54285, 54615, 54740, 54946, 55278, 55611, 55945, 56280, 56616, 56953, 57155, 57291, 57630, 57970, 58311, 58653, 58905, 58996, 59340, 59640, 59685, 60031, 60378, 60726, 61075, 61425, 61776, 62128, 62196, 62481, 62835, 63190, 63546, 63903, 64261, 64620, 64824, 64980, 65341, 65703, 65780, 66045, 66066, 66430, 66795, 67161, 67525, 67528, 67896, 68265, 68635, 69006, 69378, 69751, 70125, 70300, 70500, 70876, 71253, 71631, 72010, 72390, 72771, 73150, 73153, 73536, 73815, 73920, 74305, 74613, 74691, 75078, 75466, 75582, 75855, 76076, 76245, 76636, 77028, 77421, 77520, 77815, 78210, 78606, 79003, 79079, 79401, 79800, 80200, 80601, 80730, 81003, 81406, 81810, 82160, 82215, 82251, 82621, 83028, 83436, 83845, 84255, 84666, 85078, 85320, 85491, 85905, 86320, 86736, 87153, 87571, 87990, 88410, 88560, 88831, 89253, 89676, 90100, 90525, 90951, 91378, 91390, 91806, 91881, 92235, 92378, 92665, 93096, 93528, 93961, 94395, 94830, 95266, 95284, 95703, 96141, 96580, 97020, 97461, 97903, 98280, 98346, 98770, 98790, 99235, 99681, 100128, 100576, 100947, 101025, 101270, 101475, 101926, 102340.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 4517490 values, from 6 to 10000002437316).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 2269130 | 2248360 | 2 | ||||||||
| 3 | 2998338 | 1505013 | 14139 | 3 | |||||||
| 4 | 1144753 | 1124176 | 1124377 | 1124184 | 4 | ||||||
| 5 | 1816364 | 1797848 | 332 | 894777 | 8169 | 5 | |||||
| 6 | 1502859 | 749140 | 10398 | 1495479 | 755873 | 3741 | 6 | ||||
| 7 | 1298175 | 1284761 | 82 | 1283443 | 5676 | 645 | 644708 | 7 | |||
| 8 | 572605 | 562083 | 562188 | 562091 | 572148 | 562093 | 562189 | 562093 | 8 | ||
| 9 | 1000275 | 1495549 | 4711 | 998814 | 4710 | 4700 | 999249 | 4754 | 4728 | 9 | |
| 10 | 914283 | 896864 | 249 | 447296 | 6133 | 902081 | 900984 | 83 | 447481 | 2036 | 10 |
| 11 | 826399 | 821288 | 3937 | 813168 | 410859 | 830 | 813273 | 3655 | 38 | 3586 | 820457 |
A pictorial representation of the table above
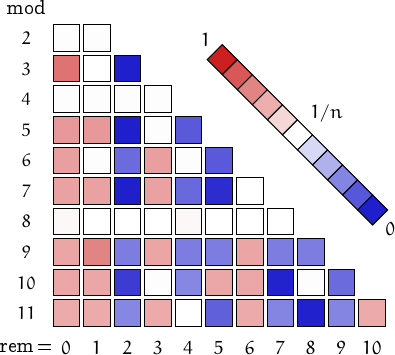
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits