• 202 can be written using four 4's:
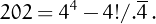
202 has 4 divisors (see below), whose sum is σ = 306. Its totient is φ = 100.
The previous prime is 199. The next prime is 211.
202 is nontrivially palindromic in base 10.
202 is digitally balanced in base 2, because in such base it contains all the possibile digits an equal number of times.
It is a semiprime because it is the product of two primes.
It can be written as a sum of positive squares in only one way, i.e., 121 + 81 = 11^2 + 9^2 .
It is a Smith number, since the sum of its digits (4) coincides with the sum of the digits of its prime factors. Since it is squarefree, it is also a hoax number.
202 is an undulating number in base 10.
It is a plaindrome in base 9, base 12 and base 13.
It is a nialpdrome in base 3, base 15 and base 16.
It is a junction number, because it is equal to n+sod(n) for n = 191 and 200.
It is not an unprimeable number, because it can be changed into a prime (2) by changing a digit.
It is a polite number, since it can be written as a sum of consecutive naturals, namely, 49 + ... + 52.
202 is a deficient number, since it is larger than the sum of its proper divisors (104).
202 is a wasteful number, since it uses less digits than its factorization.
202 is an evil number, because the sum of its binary digits is even.
The sum of its prime factors is 103.
The product of its (nonzero) digits is 4, while the sum is 4.
The square root of 202 is about 14.2126704036. The cubic root of 202 is about 5.8674643084.
It can be divided in two parts, 20 and 2, that added together give a palindrome (22).
The spelling of 202 in words is "two hundred two", and thus it is an aban number and an iban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.068 sec. • engine limits •

