• 101 can be written using four 4's:
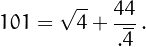
101 has 2 divisors, whose sum is σ = 102. Its totient is φ = 100.
The previous prime is 97. The next prime is 103.
It is an alternating factorial (101 = 5! - 4! + 3! - 2! + 1!).
101 is nontrivially palindromic in base 10.
It is a Cunningham number, because it is equal to 102+1.
101 is an esthetic number in base 10 and base 16, because in such bases its adjacent digits differ by 1.
It is an a-pointer prime, because the next prime (103) can be obtained adding 101 to its sum of digits (2).
It is a strong prime.
It can be written as a sum of positive squares in only one way, i.e., 100 + 1 = 10^2 + 1^2 .
It is a palprime.
It is a sliding number, since 101 = 1 + 100 and 1/1 + 1/100 = 1.01.
It is a cyclic number.
It is not a de Polignac number, because 101 - 22 = 97 is a prime.
Together with 103, it forms a pair of twin primes.
It is a Chen prime.
It is a magnanimous number.
It is an alternating number because its digits alternate between odd and even.
101 is a strobogrammatic number because it is the same when read upside-down.
101 is an undulating number in base 10.
It is a partition number, being equal to the number of ways a set of 13 identical objects can be partitioned into subset.
It is a plaindrome in base 6, base 8, base 9, base 13 and base 15.
It is a nialpdrome in base 11, base 12, base 14 and base 16.
It is a junction number, because it is equal to n+sod(n) for n = 91 and 100.
It is a congruent number.
It is a good prime.
It is a polite number, since it can be written as a sum of consecutive naturals, namely, 50 + 51.
It is an arithmetic number, because the mean of its divisors is an integer number (51).
101 is the 5-th centered decagonal number.
It is an amenable number.
101 is a deficient number, since it is larger than the sum of its proper divisors (1).
101 is an equidigital number, since it uses as much as digits as its factorization.
101 is an evil number, because the sum of its binary digits is even.
The product of its (nonzero) digits is 1, while the sum is 2.
The square root of 101 is about 10.0498756211. The cubic root of 101 is about 4.6570095078.
It can be divided in two parts, 10 and 1, that added together give a palindrome (11).
The spelling of 101 in words is "one hundred one", and thus it is an aban number and an iban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.069 sec. • engine limits •

