• 251 can be written using four 4's:
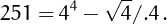
251 has 2 divisors, whose sum is σ = 252. Its totient is φ = 250.
The previous prime is 241. The next prime is 257. The reversal of 251 is 152.
251 is nontrivially palindromic in base 8.
It is a strong prime.
It is a cyclic number.
It is a trimorphic number since its cube, 15813251, ends in 251.
It is a de Polignac number, because none of the positive numbers 2k-251 is a prime.
It is a Sophie Germain prime.
It is a Chen prime.
251 is an undulating number in base 8.
It is a plaindrome in base 12, base 14 and base 15.
It is a nialpdrome in base 16.
It is not a weakly prime, because it can be changed into another prime (257) by changing a digit.
It is a pernicious number, because its binary representation contains a prime number (7) of ones.
It is a good prime.
It is a polite number, since it can be written as a sum of consecutive naturals, namely, 125 + 126.
It is an arithmetic number, because the mean of its divisors is an integer number (126).
2251 is an apocalyptic number.
251 is a deficient number, since it is larger than the sum of its proper divisors (1).
251 is an equidigital number, since it uses as much as digits as its factorization.
251 is an odious number, because the sum of its binary digits is odd.
The product of its digits is 10, while the sum is 8.
The square root of 251 is about 15.8429795178. The cubic root of 251 is about 6.3079935487.
Subtracting from 251 its reverse (152), we obtain a palindrome (99).
The spelling of 251 in words is "two hundred fifty-one", and thus it is an aban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.081 sec. • engine limits •

