• 336 can be written using four 4's:
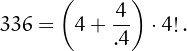
336 has 20 divisors (see below), whose sum is σ = 992. Its totient is φ = 96.
The previous prime is 331. The next prime is 337. The reversal of 336 is 633.
336 is an esthetic number in base 5, because in such base its adjacent digits differ by 1.
It is a super-2 number, since 2×3362 = 225792, which contains 22 as substring.
It is a hoax number, since the sum of its digits (12) coincides with the sum of the digits of its distinct prime factors.
It is a Harshad number since it is a multiple of its sum of digits (12).
It is a nude number because it is divisible by every one of its digits.
Its product of digits (54) is a multiple of the sum of its prime factors (18).
It is a plaindrome in base 10.
It is a nialpdrome in base 4, base 7 and base 8.
It is a zygodrome in base 4.
It is a congruent number.
It is not an unprimeable number, because it can be changed into a prime (331) by changing a digit.
336 is an untouchable number, because it is not equal to the sum of proper divisors of any number.
It is a pernicious number, because its binary representation contains a prime number (3) of ones.
It is a polite number, since it can be written in 3 ways as a sum of consecutive naturals, for example, 45 + ... + 51.
It is an amenable number.
It is a practical number, because each smaller number is the sum of distinct divisors of 336, and also a Zumkeller number, because its divisors can be partitioned in two sets with the same sum (496).
336 is an abundant number, since it is smaller than the sum of its proper divisors (656).
It is a pseudoperfect number, because it is the sum of a subset of its proper divisors.
336 is a wasteful number, since it uses less digits than its factorization.
336 is an odious number, because the sum of its binary digits is odd.
The sum of its prime factors is 18 (or 12 counting only the distinct ones).
The product of its digits is 54, while the sum is 12.
The square root of 336 is about 18.3303027798. The cubic root of 336 is about 6.9520532898.
Subtracting from 336 its sum of digits (12), we obtain a square (324 = 182).
336 divided by its sum of digits (12) gives a triangular number (28 = T7).
Subtracting from 336 its product of digits (54), we obtain a palindrome (282).
Adding to 336 its reverse (633), we get a palindrome (969).
The spelling of 336 in words is "three hundred thirty-six", and thus it is an aban number and an oban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.071 sec. • engine limits •

