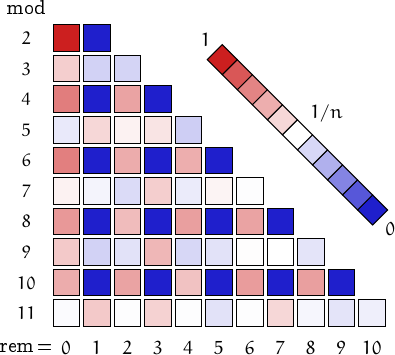
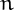 is called untouchable if it is not the sum of the proper divisors of any number, i.e. if it does not exist a number
is called untouchable if it is not the sum of the proper divisors of any number, i.e. if it does not exist a number
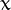 such that
such that 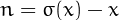 .
.
For example, 2 is untouchable because 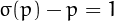 for every prime
for every prime 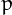 ,
and it is easy to see that
,
and it is easy to see that 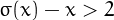 for every composite.
On the contrary, 10 is not untouchable because the proper divisors of 14
are 1, 2, and 7, and 1 + 2 + 7 = 10.
for every composite.
On the contrary, 10 is not untouchable because the proper divisors of 14
are 1, 2, and 7, and 1 + 2 + 7 = 10.
Erdős has proved that there are infinitely many untouchable numbers.
If, as it is conjectured, every even number 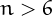 is the sum of two
distinct primes,
is the sum of two
distinct primes, 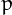 ,
, 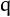 , then 5 is the only odd untouchable number,
since every larger odd number can be espressed as
, then 5 is the only odd untouchable number,
since every larger odd number can be espressed as 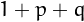 and thus
be equal to the sum of the proper divisors of
and thus
be equal to the sum of the proper divisors of 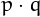 .
.
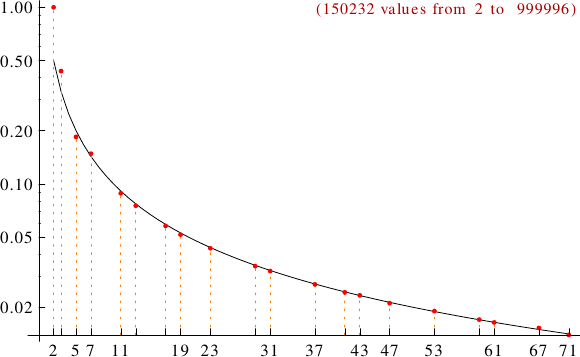
The first untouchable numbers are 2, 5, 52, 88, 96, 120, 124, 146, 162, 188, 206, 210, 216, 238, 246, 248, 262, 268, 276, 288, 290, 292, 304 more terms
You can download a text
file (untouchable_up1e6.txt) of 1.9 MB, containing a list of the 150232 untouchable numbers up to 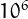 .
.