Two numbers 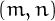 form a betrothed pair if the sum of nontrivial divisors of one number equals the other, i.e., if
form a betrothed pair if the sum of nontrivial divisors of one number equals the other, i.e., if 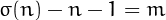 and
and 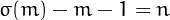 .
.
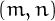 form a betrothed pair if the sum of nontrivial divisors of one number equals the other, i.e., if
form a betrothed pair if the sum of nontrivial divisors of one number equals the other, i.e., if 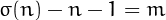 and
and 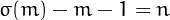 .
.
The first numbers which belong to a betrothed pair are (48, 75), (140, 195), (1050, 1925), (1575, 1648), (2024, 2295), (5775, 6128), (8892, 16587), (9504, 20735), (62744, 75495), (186615, 206504) more terms
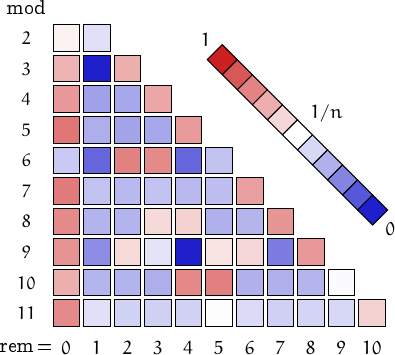
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

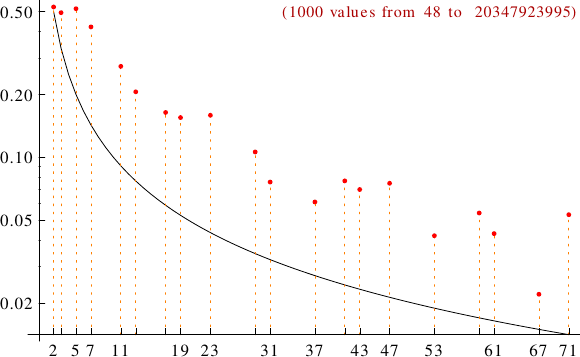
A graph displaying how many betrothed numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Betrothed numbers can also be... (you may click on names or numbers and on + to get more values)
aban
48
75
140
195
1000824
1010000396
2359000280
abundant
48
140
1050
1575
2024
5775
8892
9504
62744
186615
+
41137620
49217084
admirable
140
alternating
1050
16587
amenable
48
140
1648
1925
2024
6128
8892
9504
62744
196664
+
987558704
991087064
apocalyptic
1925
2024
5775
6128
8892
9504
16587
20735
arithmetic
140
195
1050
1925
2024
2295
5775
9504
20735
62744
+
9247095
9345903
binomial
2024
congruent
1575
1648
1925
2295
5775
6128
8892
20735
62744
75495
+
9247095
9345903
constructible
48
Cunningham
48
195
2024
5775
20735
309135
26409320
Curzon
1925
1279950
2576945
7875450
16381925
23939685
175742294
D-number
195
deficient
75
195
1648
1925
2295
6128
16587
20735
75495
206504
+
7890575
9345903
dig.balanced
75
195
8892
16587
62744
587460
2421704
4012184
5644415
9247095
+
178415048
184191111
double fact.
48
Duffinian
75
1575
1925
16587
2576945
evil
48
75
195
1050
1575
1925
2295
5775
6128
9504
+
949977644
953056175
fibodiv
75
Friedman
186615
gapful
140
195
1050
1575
5775
186615
199760
219975
266000
1140020
+
20247751575
20322463175
happy
1575
549219
587460
2576945
3220119
7509159
7890575
harmonic
140
Harshad
48
140
195
1050
2024
9504
62744
266000
312620
573560
+
9456738444
9629379500
highly composite
48
hoax
507759
549219
1057595
2198504
2681019
6618080
12146750
37291625
52389315
66275384
84854315
iban
140
2024
idoneal
48
inconsummate
75
195
16587
206504
219975
266000
309135
544784
549219
interprime
195
1050
1575
2295
9504
2140215
2312024
3676491
4282215
7875450
+
93993830
96751395
Jordan-Polya
48
junction
312620
1348935
1763019
2140215
2226014
2576945
2681019
4311024
6446325
88567059
katadrome
75
lucky
75
195
1575
186615
526575
1459143
2140215
2142945
3010215
3220119
3676491
Lynch-Bell
48
metadrome
48
modest
1648
Moran
195
nialpdrome
75
nonagonal
75
11145066075
nude
48
1575
5775
O'Halloran
140
oban
75
odious
140
1648
2024
8892
196664
219975
526575
573560
817479
1000824
+
987827555
991087064
palindromic
5775
pandigital
75
2573840619
partition
1575
pernicious
48
140
1648
2024
8892
196664
219975
573560
817479
1000824
+
8829792
9247095
plaindrome
48
practical
48
140
1050
2024
8892
9504
62744
196664
199760
266000
+
7875450
8829792
prim.abundant
1575
5775
pseudoperfect
48
140
1050
1575
2024
5775
8892
9504
62744
186615
+
573560
587460
repfigit
75
self
75
16587
196664
544784
1173704
3010215
8713880
23939685
26409320
27862695
+
548544744
987827555
Smith
507759
544784
1057595
1139144
1236536
6446325
7890575
84854315
sphenic
195
507759
super Niven
48
140
1050
super-d
1050
549219
1057595
1524831
1763019
2681019
3010215
3220119
7890575
superabundant
48
tau
8892
9504
199760
266000
2580864
6081680
8829792
14371104
94713300
102019644
+
226964240
313472880
tetrahedral
2024
trimorphic
75
uban
48
75
Ulam
48
1648
16587
196664
1139144
1173704
2142945
2198504
3123735
unprimeable
1648
1925
9504
75495
199760
1057595
1081184
1140020
1233056
1279950
+
8829792
9247095
untouchable
2024
8892
9504
199760
266000
wasteful
48
75
140
195
1050
1575
1648
1925
2024
2295
+
9247095
9345903
Zuckerman
1575
Zumkeller
48
140
1050
1575
2024
5775
8892
9504
62744