
A plot of the Ulam numbers up to 1082, arranged line by line in a
square 108×108. The plot evidentiates the peaks
in their density that occur with a frequency roughly equal
to 108/5=21.6.
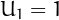 ,
, 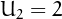 and, for
and, for 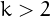 ,
, 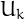 is the smallest integer that can be written in exactly one way as
is the smallest integer that can be written in exactly one way as 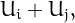 with
with 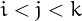 .
.
The members of the Ulam sequence are called Ulam numbers.
For example, after the first 4 terms which are trivially 1, 2, 3 and 4, the value of 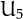 cannot be 5, since
cannot be 5, since 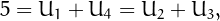 but it is 6, which can be obtained only as
but it is 6, which can be obtained only as 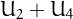 (not as
(not as  because the terms added must be distinct).
because the terms added must be distinct).
The sequence is infinite because 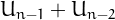 is always a viable candidate for
is always a viable candidate for 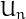 .
.
Ulam numbers are not distributed uniformly, but their density has peaks at an average distance of 21.6 (see picture above).
The first Ulam numbers are 1, 2, 3, 4, 6, 8, 11, 13, 16, 18, 26, 28, 36, 38, 47, 48, 53, 57, 62, 69, 72, 77, 82, 87, 97, 99, 102 more terms
Below, the spiral pattern of Ulam numbers up to 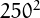 . See the page on prime numbers for an explanation and links to similar pictures.
. See the page on prime numbers for an explanation and links to similar pictures.
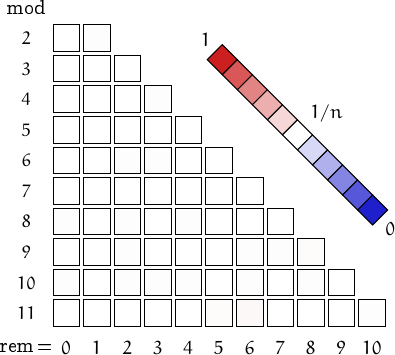
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

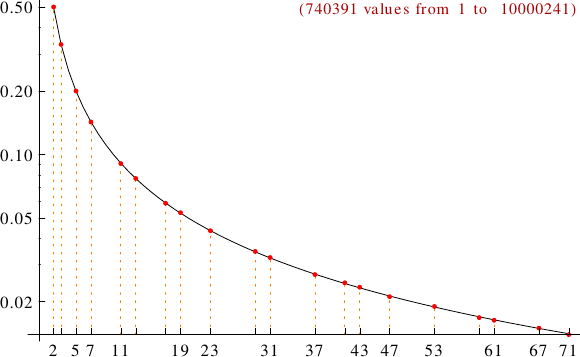
A graph displaying how many Ulam numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Ulam numbers can also be... (you may click on names or numbers and on + to get more values)
a-pointer
11
13
2633
+
9902293
ABA
18
72
324
+
9990450
aban
11
13
16
+
10000241
abundant
18
36
48
+
10000236
Achilles
72
800
864
+
9980928
admirable
102
114
138
+
9999762
alternating
16
18
36
+
9898545
amenable
13
16
28
+
10000241
amicable
5020
308620
399592
+
6377175
apocalyptic
243
382
390
+
29987
arithmetic
11
13
38
+
9999999
astonishing
429
3591
balanced p.
53
607
1103
+
9992681
bemirp
168601
1606081
betrothed
48
1648
16587
+
3123735
binomial
28
36
126
+
9956953
brilliant
209
221
253
+
10000153
c.decagonal
11
451
781
+
9947551
c.heptagonal
106
148
197
+
9919603
c.nonagonal
28
253
820
+
9956953
c.octagonal
441
2809
3481
+
9690769
c.pentagonal
16
106
456
+
9935106
c.square
13
145
221
+
9790313
c.triangular
316
409
1489
+
9934354
cake
26
5489
27776
+
9886826
Carmichael
41041
101101
294409
+
6733693
Carol
47
Catalan
429
Chen
11
13
47
+
9999161
congruent
13
28
38
+
9999999
constructible
16
48
102
+
8421376
cube
19683
97336
175616
+
8000000
Cunningham
26
28
48
+
9999999
Curzon
18
26
53
+
10000214
cyclic
11
13
47
+
9999977
D-number
57
69
87
+
7042683
d-powerful
175
209
370
+
9998724
de Polignac
905
1985
2789
+
10000109
decagonal
126
175
370
+
9729720
deceptive
451
4187
7471
+
9895217
deficient
11
13
16
+
9999999
dig.balanced
11
38
99
+
10000241
double fact.
48
46080
droll
72
800
5184
+
9461760
Duffinian
16
36
57
+
9999977
eban
36
62
2032
+
6066046
economical
11
13
16
+
10000241
emirp
13
97
739
+
9999337
emirpimes
26
62
155
+
10000153
enlightened
25000
119911
2500000
5117695
equidigital
11
13
16
+
10000241
eRAP
4233
61456
71284
+
9695764
esthetic
87
434
456
+
8787898
Eulerian
11
26
57
+
2097130
evil
18
36
48
+
10000241
factorial
720
fibodiv
28
47
497
+
2472712
Fibonacci
13
2584
514229
Friedman
126
688
1296
+
997246
frugal
243
1536
1792
+
9998677
gapful
180
253
260
+
10000214
good prime
11
53
97
+
9992681
happy
13
28
82
+
9999760
harmonic
28
8128
18620
360360
Harshad
18
36
48
+
10000236
heptagonal
18
148
189
+
9927133
hex
1387
9577
9919
+
9975457
hexagonal
28
861
1035
+
9827961
highly composite
36
48
180
+
7207200
hoax
319
382
456
+
9997800
Hogben
13
57
241
+
9894171
Honaker
131
1433
4153
+
9973021
house
155
434
4390
+
8841922
hungry
161449
712201
hyperperfect
28
8128
51301
+
4013833
iban
11
47
72
+
777722
iccanobiF
13
792517
idoneal
13
16
18
+
273
impolite
16
8192
inconsummate
62
431
441
+
999980
interprime
18
26
69
+
9999283
Jacobsthal
11
341
87381
699051
Jordan-Polya
16
36
48
+
8294400
junction
206
309
319
+
10000041
Kaprekar
99
142857
187110
+
9999999
katadrome
53
62
72
+
9876532
Lehmer
451
949
1387
+
9935131
Leyland
57
145
177
2012174
lonely
53
1340
15705
+
1357265
Lucas
11
18
47
+
1149851
lucky
13
69
87
+
9999823
Lynch-Bell
36
48
126
+
9283176
m-pointer
15121
19121
1111211
1111213
magic
175
260
2056
+
8889921
magnanimous
11
16
38
+
7719370
metadrome
13
16
18
+
1234578
modest
13
26
69
+
10000239
Moran
18
114
209
+
10000236
narcissistic
370
9800817
nialpdrome
11
53
62
+
9999999
nonagonal
2484
2674
9699
+
9968484
nude
11
36
48
+
9999999
O'Halloran
36
260
oban
11
13
16
+
986
octagonal
341
3605
5208
+
9792133
odious
11
13
16
+
10000175
Ormiston
19031
34613
56731
+
9961613
palindromic
11
77
99
+
9999999
palprime
11
131
10501
+
9871789
pancake
11
16
106
+
9961417
panconsummate
11
18
36
+
219
pandigital
11
99
114
+
9998037
partition
11
77
627
+
2012558
pentagonal
145
1335
3290
+
9721901
perfect
28
8128
pernicious
11
13
18
+
9999977
Perrin
209
6107
236282
Pierpont
13
97
10369
+
1990657
plaindrome
11
13
16
+
9999999
Poulet
341
1387
14491
+
9774181
power
16
36
243
+
9796900
powerful
16
36
72
+
9980928
practical
16
18
28
+
9999960
prim.abundant
18
102
114
+
9999762
prime
11
13
47
+
9999877
primeval
13
1037
1079
pronic
72
182
1406
+
9969806
Proth
13
57
97
+
9936897
pseudoperfect
18
28
36
+
1000000
repdigit
11
77
99
+
9999999
repfigit
28
47
197
+
925993
repunit
13
57
241
+
9894171
Rhonda
178754
194526
521356
+
9541116
Ruth-Aaron
16
77
126
+
9790430
Saint-Exupery
7500
14760
65520
+
9903180
Sastry
2975208
self
53
97
209
+
10000109
semiprime
26
38
57
+
10000241
sliding
11
502
5020
+
6415625
Smith
319
382
483
+
9997341
Sophie Germain
11
53
131
+
9991259
sphenic
102
114
138
+
10000239
square
16
36
324
+
9796900
star
13
253
11881
+
9639337
straight-line
258
456
864
+
9999999
strobogrammatic
11
69
986
+
9891686
strong prime
11
97
197
+
9999877
super Niven
36
48
102
+
9306000
super-d
69
106
131
+
9999569
superabundant
36
48
180
+
7207200
tau
18
36
72
+
10000236
taxicab
46683
195841
1734264
+
8587000
tetrahedral
14190
19600
50116
+
9660036
triangular
28
36
253
+
9956953
tribonacci
13
927
5768
trimorphic
99
624
751
+
9999999
truncatable prime
13
47
53
+
9966883
twin
11
13
197
+
9999161
uban
11
13
16
+
10000087
undulating
131
282
363
+
8282828
unprimeable
206
324
624
+
9999960
untouchable
206
238
324
+
999836
upside-down
28
82
258
+
9945611
vampire
126027
135837
146952
+
362992
wasteful
18
26
28
+
9999999
weak prime
13
47
131
+
9999481
weird
7192
16030
19810
+
992332
Wieferich
52665
94797
473985
Woodall
1023
49151
93749
+
9961471
Zeisel
294409
Zuckerman
11
36
175
+
9123192
Zumkeller
28
48
102
+
99774
zygodrome
11
77
99
+
9999999