 is abundant if
is abundant if 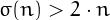 , i.e., if the sum of the proper divisors of
, i.e., if the sum of the proper divisors of 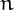 is larger than
is larger than 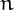 .
.
For example, 12 is abundant since the sum of its proper divisors, 1 + 2 + 3 + 4 + 6 = 16, exceeds 12 itself.
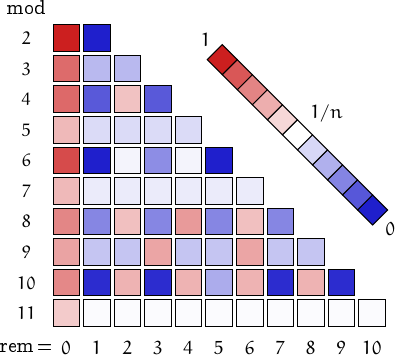
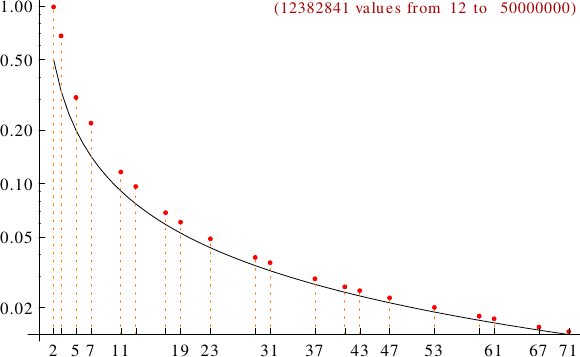
There are infinite abundant numbers since, for example, all the multiples of an abundant number is abundant. It has been estimated that about 1/4 of the integers are abundant.
It is possible to obtain abundant numbers lacking any combination of prime factors, but they grow fast, as shown in the table below.
| f | min number lacking f |
|---|---|
| 2 | 945 |
| 3 | 20 |
| 5 | 12 |
| 2 ⋅ 3 | 5391411025 |
| 2 ⋅ 5 | 81081 |
| 3 ⋅ 5 | 56 |
| 2 ⋅ 3 ⋅ 5 | 20169691981106018776756331 |
Every number greater that 991 can be expressed as the sum of abundant numbers. Two addends are sufficient for every integer greater than 20161 and for every even number greater than 46.
The smallest pair of consecutive abundant numbers is (5775, 5776).
The first such triple starts at 171078830, while the smallest known quadruple, found by Bruno Mishutka, starts at 141363708067871564084
The first abundant numbers are
12, 18, 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, 66, 70, 72, 78, 80, 84, 88, 90, 96, 100 more terms
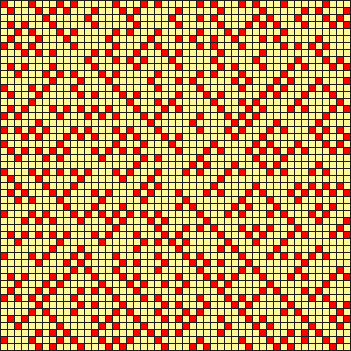
Below, the spiral pattern of abundant numbers up to 2500. See the page on prime numbers for an explanation and links to similar pictures.