A number is palindromic in base 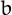 (usually base 10) if the representation in
that base is the same read from the right or from the left, as in 1257521, or in
(usually base 10) if the representation in
that base is the same read from the right or from the left, as in 1257521, or in 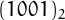 which is the representation of 9 in base 2.
which is the representation of 9 in base 2.
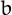 (usually base 10) if the representation in
that base is the same read from the right or from the left, as in 1257521, or in
(usually base 10) if the representation in
that base is the same read from the right or from the left, as in 1257521, or in 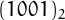 which is the representation of 9 in base 2.
which is the representation of 9 in base 2.
A palindrome is nontrivial if it has more than one digit.
The first such numbers (in base 10) are 11, 22, 33, 44, 55, 66, 77, 88, 99, 101, 111, 121, 131, 141, 151, 161, 171, 181, 191, 202 more terms
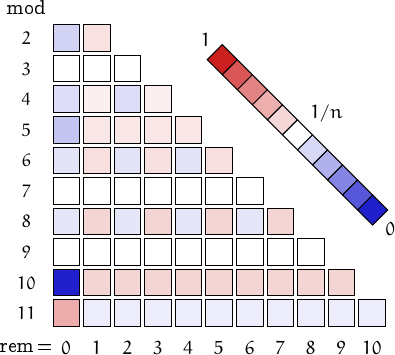
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

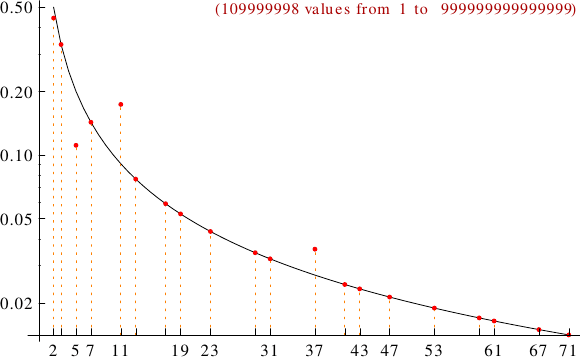
A graph displaying how many palindromic numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Useful links
Patrick De Geest, World of Numbers a website dedicated to palindromes
Mathworld, Palindromic Number
OEIS, Sequence A002113
Mathworld, Palindromic Number
OEIS, Sequence A002113
Palindromic numbers can also be... (you may click on names or numbers and on + to get more values)
a-pointer
11
101
181
+
967828769
ABA
242
3993
20402
+
8163248423618
aban
11
22
33
+
999000000999
abundant
66
88
222
+
49988994
Achilles
36963
2138312
2177712
+
40516277261504
admirable
66
88
222
+
8987898
alt.fact.
101
alternating
101
121
141
+
989898989
amenable
33
44
77
+
989999989
apocalyptic
222
434
646
+
29992
arithmetic
11
22
33
+
9999999
balanced p.
373
11411
30103
+
996989699
betrothed
5775
binomial
55
66
171
+
6874200024786
brilliant
121
323
737
+
999949999
c.decagonal
11
101
151
+
155075181570551
c.heptagonal
22
1331
1919191
+
38437311373483
c.nonagonal
55
595
5995
+
683727232727386
c.octagonal
121
10201
12321
+
900075181570009
c.pentagonal
141
181
10401
+
620873909378026
c.square
181
313
545
+
582818040818285
c.triangular
15151
45154
66466
+
479573060375974
cake
232
10701
Carmichael
101101
Carol
959
Chen
11
101
131
+
9981899
congruent
22
55
77
+
9999999
constructible
272
cube
343
1331
1030301
+
1334996994331
Cullen
161
Cunningham
33
99
101
+
995570353075599
Curzon
33
141
393
+
189959981
cyclic
11
33
77
+
9998999
D-number
33
111
141
+
7023207
d-powerful
262
333
373
+
9859589
de Polignac
373
757
959
+
99944999
decagonal
232
27972
76867
+
675972505279576
deceptive
7777
10001
11111
+
35300000353
deficient
11
22
33
+
9999999
dig.balanced
11
44
99
+
199505991
droll
4224
48384
Duffinian
55
77
111
+
9998999
eban
44
66
2002
+
66066066066066
economical
11
101
111
+
18800881
enlightened
119911
equidigital
11
101
111
+
18800881
eRAP
23444432
3686336863
98784948789
802959959208
esthetic
101
121
212
+
989898989898989
Eulerian
11
66
evil
33
66
77
+
1000000001
fibodiv
323
646
969
Fibonacci
55
Friedman
121
343
10201
+
825528
frugal
343
1331
10201
+
985383589
gapful
121
242
363
+
99990009999
Giuga
858
good prime
11
101
191
+
195353591
happy
44
262
313
+
9992999
Harshad
111
171
222
+
8998558998
heptagonal
55
616
3553
+
717685292586717
hex
919
1081801
1188811
+
131374494473131
hexagonal
66
3003
5995
+
636188414881636
hoax
22
202
424
+
98122189
Hogben
111
343
757
+
755971313179557
Honaker
131
16661
33533
+
982323289
house
434
28882
339585933
iban
11
22
44
+
777777
idoneal
22
33
88
232
inconsummate
161
272
383
+
969969
insolite
111
111111111
interprime
99
111
282
+
99755799
Jacobsthal
11
171
junction
101
111
202
+
94999949
Kaprekar
55
99
999
+
999999999999999
Lehmer
595
949
1111
+
153452254351
Lucas
11
167761
lucky
33
99
111
+
9986899
m-pointer
131121131
1116111116111
magic
111
505
5335
magnanimous
11
101
1001
modest
111
222
333
+
1999889991
Moran
111
171
222
+
89888898
Motzkin
323
nialpdrome
11
22
33
+
999999999999999
nonagonal
111
474
969
+
699030030996
nude
11
22
33
+
489939984
O'Halloran
44
oban
11
33
55
+
999
octagonal
8008
120232021
124060421
+
12212500521221
odious
11
22
44
+
999999999
Ormiston
1303031
1333331
1360631
+
977999779
palprime
11
101
131
+
999999787999999
pancake
11
22
121
+
706625414526607
panconsummate
11
77
121
353
pandigital
11
99
141
+
298989892
partition
11
22
77
101
pentagonal
22
1001
2882
+
264571020175462
pernicious
11
22
33
+
9998999
Perrin
22
plaindrome
11
22
33
+
999999999999999
Poulet
101101
129921
1837381
power
121
343
484
+
9420645460249
powerful
121
343
484
+
900075181570009
practical
66
88
252
+
8992998
prim.abundant
66
88
222
+
97922979
prime
11
101
131
+
99999199999
pronic
272
6006
289982
+
250087292780052
Proth
33
161
353
+
946783387649
pseudoperfect
66
88
222
+
999999
repdigit
11
22
33
+
999999999999999
repunit
111
121
343
+
755971313179557
Rhonda
512219912215
Ruth-Aaron
77
949
1331
+
804939939408
self
121
222
323
+
999939999
self-describing
22
4444
442244
+
88886666668888
semiprime
22
33
55
+
99977999
sliding
11
101
1001
+
100000000000001
Smith
22
121
202
+
99144199
Sophie Germain
11
131
191
+
999212999
sphenic
66
222
282
+
99988999
square
121
484
676
+
900075181570009
star
121
181
1441
+
396868131868693
straight-line
111
222
333
+
999999999999999
strobogrammatic
11
88
101
+
888888888888888
strong prime
11
101
191
+
9980899
subfactorial
44
super-d
131
181
333
+
9990999
tau
88
232
252
+
889949988
taxicab
4607064
2344344434432
109514040415901
tetrahedral
969
1771
6378736
triangular
55
66
171
+
684866959668486
tribonacci
44
trimorphic
99
999
9999
+
999999999999999
truncatable prime
313
353
373
+
799636997
twin
11
101
151
+
999454999
uban
11
22
33
+
99000099000099
Ulam
11
77
99
+
9999999
undulating
101
121
131
+
989898989898989
unprimeable
515
535
626
+
8997998
untouchable
88
262
292
+
890098
upside-down
55
555
5555
+
555555555555555
wasteful
22
33
44
+
9999999
weak prime
131
151
181
+
9989899
weakly prime
79856965897
91507670519
Woodall
191
323
383
99999999999
Zuckerman
11
111
212
+
2321111232
Zumkeller
66
88
222
+
89898
zygodrome
11
22
33
+
999999999999999