The Gauss-Wantzel theorem states that a regular polygon with 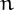 sides
can be constructed with ruler and compass if and only if
sides
can be constructed with ruler and compass if and only if
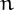 can be written as
can be written as 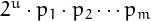 , where
, where 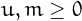 and
the
and
the 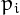 's are distinct Fermat primes, that is primes of the form
's are distinct Fermat primes, that is primes of the form 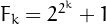 .
.
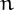 sides
can be constructed with ruler and compass if and only if
sides
can be constructed with ruler and compass if and only if
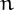 can be written as
can be written as 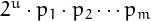 , where
, where 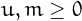 and
the
and
the 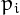 's are distinct Fermat primes, that is primes of the form
's are distinct Fermat primes, that is primes of the form 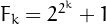 .
.
Note that only 5 Fermat primes are known, namely, 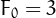 ,
, 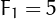 ,
,
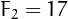 ,
, 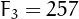 , and
, and 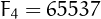 .
.
A.M.Gleason has proved that
if the use of the angle-trisector is allowed,
then the constructible polygons have
sides of the form 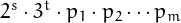 ,
where the
,
where the 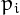 's are distinct Pierpont primes.
's are distinct Pierpont primes.
The first 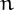 such that a regular polygon with
such that a regular polygon with 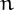 sides can be
constructed with ruler and compass are
3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102 more terms
sides can be
constructed with ruler and compass are
3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102 more terms
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

Constructible polygons can also be... (you may click on names or numbers and on + to get more values)
ABA
24
32
64
+
8796093022208
aban
10
12
15
+
960
abundant
12
20
24
+
44738560
admirable
12
20
24
+
393222
alternating
10
12
16
+
69632
amenable
12
16
17
+
858980352
apocalyptic
192
384
1088
+
26214
arithmetic
15
17
20
+
6684774
astonishing
15
204
balanced p.
257
Bell
15
betrothed
48
binomial
10
15
20
+
2147516416
brilliant
10
15
c.nonagonal
10
136
32896
2147516416
c.pentagonal
16
51
2176
c.square
85
c.triangular
10
64
85
+
514
cake
15
64
2048
82240
Chen
17
257
65537
compositorial
24
192
congruent
15
20
24
+
8912896
cube
64
512
4096
+
281474976710656
Cunningham
10
15
17
+
17180131328
Curzon
30
510
8738
+
6684774
cyclic
15
17
51
+
5570645
D-number
15
51
771
196611
d-powerful
24
1542
2048
+
7864320
de Polignac
16843009
decagonal
10
85
deficient
10
15
16
+
8913032
dig.balanced
10
12
15
+
178257920
double fact.
15
48
384
3840
droll
240
52224
174080
Duffinian
16
32
64
+
8388608
eban
30
32
34
+
2056
economical
10
15
16
+
17895424
emirp
17
emirpimes
15
51
85
+
1114129
enlightened
256
2048
2176
+
274877906944
equidigital
10
15
16
+
17895424
eRAP
20
24
170
esthetic
10
12
32
34
Eulerian
120
evil
10
12
15
+
858993459
factorial
24
120
Fibonacci
34
Friedman
128
1024
1285
+
983040
frugal
128
256
512
+
855638016
gapful
120
160
170
+
86236206080
Giuga
30
good prime
17
257
65537
happy
10
32
68
+
8912896
Harshad
10
12
20
+
8589803520
heptagonal
34
hexagonal
15
120
32640
2147450880
highly composite
12
24
48
+
240
hoax
85
136
160
+
53478192
house
32
1285
hungry
17
iban
10
12
17
+
41120
iccanobiF
514
idoneal
10
12
15
+
408
impolite
16
32
64
+
562949953421312
inconsummate
272
771
816
+
983055
interprime
12
15
30
+
63160320
Jacobsthal
85
21845
1431655765
Jordan-Polya
12
16
24
+
844424930131968
junction
204
408
816
+
84215045
katadrome
10
20
30
+
960
Lehmer
15
51
85
+
4294967295
Leyland
17
32
320
+
281479271677952
lonely
120
lucky
15
51
1285
983055
Lynch-Bell
12
15
24
+
3264
magic
15
34
2056
8388736
magnanimous
12
16
20
+
512
metadrome
12
15
16
+
257
Motzkin
51
nialpdrome
10
20
30
+
7710
nonagonal
24
204
nude
12
15
24
+
26843136
O'Halloran
12
20
60
204
oban
10
12
15
+
960
octagonal
40
96
408
odious
16
32
64
+
536870912
palindromic
272
pancake
16
4096
panconsummate
10
12
15
+
257
pandigital
15
120
20560
30720
partition
15
30
pentagonal
12
51
pernicious
10
12
17
+
8912896
Perrin
10
12
17
+
68
Pierpont
17
257
65537
plaindrome
12
15
16
+
12336
Poulet
4369
16843009
power
16
32
64
+
35184372088832
powerful
16
32
64
+
562949953421312
practical
12
16
20
+
8947712
prim.abundant
12
20
30
+
393222
prime
17
257
65537
primorial
30
pronic
12
20
30
+
4295032832
Proth
17
257
65537
pseudoperfect
12
20
24
+
986880
repunit
15
40
85
+
4294967295
Ruth-Aaron
15
16
24
Saint-Exupery
60
480
2040
+
281470681743360
self
20
64
255
+
855651072
semiprime
10
15
34
+
16843009
sliding
20
Smith
85
4369
32896
+
786444
sphenic
30
102
170
+
84215045
square
16
64
256
+
281474976710656
strobogrammatic
96
strong prime
17
65537
super Niven
10
12
20
+
4080
super-d
3084
3855
4369
+
8355840
superabundant
12
24
48
+
240
tau
12
24
40
+
858980352
tetrahedral
10
20
120
+
46912496107520
tetranacci
15
triangular
10
15
120
+
2147516416
tribonacci
24
trimorphic
24
51
truncatable prime
17
twin
17
65537
uban
10
12
15
+
96
Ulam
16
48
102
+
8421376
undulating
272
unprimeable
204
320
510
+
8947712
untouchable
96
120
408
+
986880
upside-down
64
8192
wasteful
12
20
24
+
8947712
Woodall
17
80
Zuckerman
12
15
24
+
2228224
Zumkeller
12
20
24
+
98688