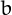 (often 10 or 16)
if its digits are in nonincreasing order in that base.
(often 10 or 16)
if its digits are in nonincreasing order in that base.
For example, 43210, 2222, 76652 and 9630 are all nialpdromes in base 10.
A nialpdrome in which the digits are strictly decreasing is called katadrome, while numbers whose digits are deincreasing and strictly decreasing are called plaindromes and metadromes.
The number 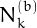 of nialpdromes of
of nialpdromes of  digits in base
digits in base 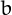 is equal to
is equal to
![\[
N^{(b)}_k = {{k+b-1}\choose {b-1}}-1\,,
\]](pic.4.png)
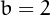 simplifies to
simplifies to 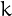 . In general
. In general 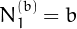 , since we count also the 0 among the 1-digit nialpdromes.
, since we count also the 0 among the 1-digit nialpdromes.
The total number 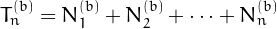 of nialpdromes in base
of nialpdromes in base 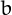 with at most
with at most 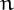 digits is equal to
digits is equal to
![\[
T^{(b)}_n = {{n+b}\choose{n}}-n\,.
\]](pic.10.png)
Probably the largest nialpdrome primes with index respectively
nialpdrome and plaindrome are 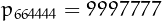 and
and 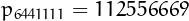 .
See the plaindromes for the symmetric pairs.
.
See the plaindromes for the symmetric pairs.
The first nialpdromes (in base 10) are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 20, 21, 22, 30, 31, 32, 33, 40, 41, 42, 43, 44, 50 more terms
Below, the spiral pattern of nialpdromes up to 10000 . See the page on prime numbers for an explanation and links to similar pictures.

OEIS, Sequence A009996 (base 10)
OEIS, Sequence A023771 (base 16)