• 132 can be written using four 4's:
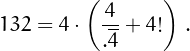
132 has 12 divisors (see below), whose sum is σ = 336. Its totient is φ = 40.
The previous prime is 131. The next prime is 137. The reversal of 132 is 231.
132 is an esthetic number in base 5, because in such base its adjacent digits differ by 1.
It is a tau number, because it is divible by the number of its divisors (12).
It is the 6-th Catalan number.
It is a Harshad number since it is a multiple of its sum of digits (6).
It is a nude number because it is divisible by every one of its digits and also a Zuckerman number because it is divisible by the product of its digits.
It is a d-powerful number, because it can be written as 1 + 3 + 27 .
It is one of the 548 Lynch-Bell numbers.
It is a plaindrome in base 7, base 9 and base 15.
It is a nialpdrome in base 11, base 12, base 13, base 14 and base 16.
It is a self number, because there is not a number n which added to its sum of digits gives 132.
It is a pernicious number, because its binary representation contains a prime number (2) of ones.
It is a polite number, since it can be written in 3 ways as a sum of consecutive naturals, for example, 7 + ... + 17.
It is an arithmetic number, because the mean of its divisors is an integer number (28).
132 is a gapful number since it is divisible by the number (12) formed by its first and last digit.
It is a pronic number, being equal to 11×12.
It is an amenable number.
It is a practical number, because each smaller number is the sum of distinct divisors of 132, and also a Zumkeller number, because its divisors can be partitioned in two sets with the same sum (168).
132 is an abundant number, since it is smaller than the sum of its proper divisors (204).
It is a pseudoperfect number, because it is the sum of a subset of its proper divisors.
132 is a wasteful number, since it uses less digits than its factorization.
132 is an evil number, because the sum of its binary digits is even.
The sum of its prime factors is 18 (or 16 counting only the distinct ones).
The product of its digits is 6, while the sum is 6.
The square root of 132 is about 11.4891252931. The cubic root of 132 is about 5.0916433697.
Adding to 132 its reverse (231), we get a palindrome (363).
Subtracting 132 from its reverse (231), we obtain a palindrome (99).
It can be divided in two parts, 13 and 2, that added together give a triangular number (15 = T5).
The spelling of 132 in words is "one hundred thirty-two", and thus it is an aban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.033 sec. • engine limits •

