• 53 can be written using four 4's:
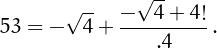
53 has 2 divisors, whose sum is σ = 54. Its totient is φ = 52.
The previous prime is 47. The next prime is 59. The reversal of 53 is 35.
53 is an esthetic number in base 8 and base 12, because in such bases its adjacent digits differ by 1.
It is a balanced prime because it is at equal distance from previous prime (47) and next prime (59).
It can be written as a sum of positive squares in only one way, i.e., 49 + 4 = 7^2 + 2^2 .
53 is a truncatable prime.
It is a cyclic number.
It is not a de Polignac number, because 53 - 24 = 37 is a prime.
It is a Sophie Germain prime.
It is a Chen prime.
It is an Ulam number.
It is a lonely number, since its distance to closest prime (59) sets a new record.
It is a Curzon number.
It is a plaindrome in base 3, base 6, base 9, base 11, base 12, base 14, base 15 and base 16.
It is a nialpdrome in base 4, base 8, base 10 and base 13.
It is a self number, because there is not a number n which added to its sum of digits gives 53.
It is a congruent number.
It is a panconsummate number.
It is a good prime.
It is a polite number, since it can be written as a sum of consecutive naturals, namely, 26 + 27.
It is an arithmetic number, because the mean of its divisors is an integer number (27).
It is an amenable number.
53 is a deficient number, since it is larger than the sum of its proper divisors (1).
53 is an equidigital number, since it uses as much as digits as its factorization.
It is an anagram of its base 16 representation: 53 = (35)16.
53 is an evil number, because the sum of its binary digits is even.
The product of its digits is 15, while the sum is 8.
The square root of 53 is about 7.2801098893. The cubic root of 53 is about 3.7562857542.
Adding to 53 its reverse (35), we get a palindrome (88).
The spelling of 53 in words is "fifty-three", and thus it is an aban number, an oban number, and an uban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.708 sec. • engine limits •

