The subfactorial of an integer 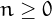 , often denoted by
, often denoted by 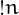 is equal to the number of derangements of
is equal to the number of derangements of 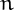 objects, i.e., the number of permutations with no fixed points.
objects, i.e., the number of permutations with no fixed points.
![\[
!n = n!\sum_{i=0}^{n}\frac{(-1)^i}{i!}\, =\, \sum_{k=0}^n(-1)^{n-k}k!{n\choose k}\, =\, \left\lfloor\frac{n!+1}{e}\right\rfloor\,,
\]](pic.15.png) where the last formula holds for
where the last formula holds for 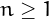 .
.
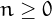 , often denoted by
, often denoted by 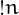 is equal to the number of derangements of
is equal to the number of derangements of 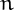 objects, i.e., the number of permutations with no fixed points.
objects, i.e., the number of permutations with no fixed points.
For example 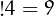 , because there are 9 derangments of the set
, because there are 9 derangments of the set 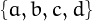 , namely
, namely 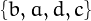 ,
, 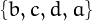 ,
, 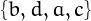 ,
,  ,
, 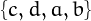 ,
,
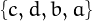 ,
, 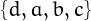 ,
, 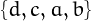 , and
, and 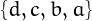 .
.
Three formulas for 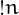 :
:
![\[
!n = n!\sum_{i=0}^{n}\frac{(-1)^i}{i!}\, =\, \sum_{k=0}^n(-1)^{n-k}k!{n\choose k}\, =\, \left\lfloor\frac{n!+1}{e}\right\rfloor\,,
\]](pic.15.png)
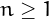 .
.
The first subfactorials are 1, 0, 1, 2, 9, 44, 265, 1854, 14833, 133496, 1334961, 14684570, 176214841, 2290792932, 32071101049, 481066515734 more terms
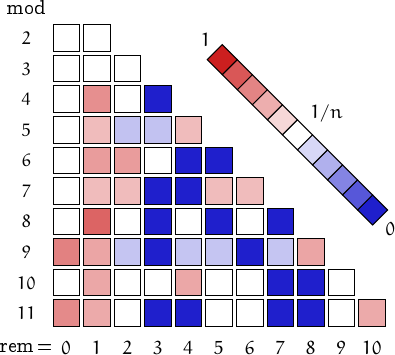
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

A graph displaying how many subfactorials are multiples of the primes p from 2 to 71. In black the ideal line 1/p.
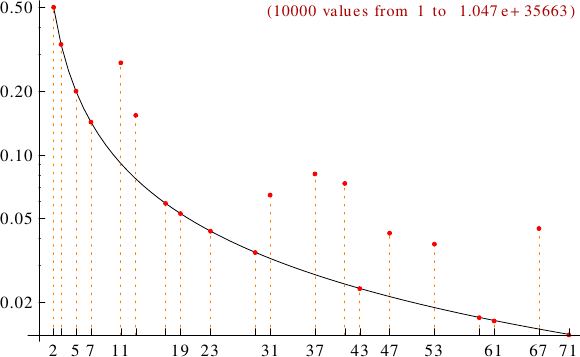

Subfactorials can also be... (you may click on names or numbers)
aban
44
265
abundant
1854
133496
alternating
1854
amenable
44
265
14833
133496
1334961
176214841
apocalyptic
14833
arithmetic
44
265
1854
14833
c.square
265
congruent
265
1854
133496
Curzon
1854
cyclic
265
14833
deficient
44
265
14833
1334961
dig.balanced
44
Duffinian
265
eban
44
economical
265
1334961
emirpimes
265
equidigital
265
1334961
evil
1854
176214841
gapful
14833
14684570
176214841
happy
44
Harshad
1854
1334961
hoax
265
iban
44
interprime
1854
133496
Lehmer
14833
magnanimous
265
modest
1854
Moran
1854
mountain
265
1854
nialpdrome
44
nude
44
O'Halloran
44
odious
44
265
14833
133496
1334961
14684570
palindromic
44
pernicious
44
265
133496
1334961
plaindrome
44
practical
133496
pseudoperfect
1854
133496
repdigit
44
self
14833
14684570
semiprime
265
Smith
265
sphenic
14833
14684570
tribonacci
44
unprimeable
1854
wasteful
44
1854
14833
133496
zygodrome
44