• 102 can be written using four 4's:
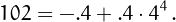
102 has 8 divisors (see below), whose sum is σ = 216. Its totient is φ = 32.
The previous prime is 101. The next prime is 103. The reversal of 102 is 201.
102 is nontrivially palindromic in base 16.
102 is an esthetic number in base 4 and base 9, because in such bases its adjacent digits differ by 1.
It is an interprime number because it is at equal distance from previous prime (101) and next prime (103).
It is a sphenic number, since it is the product of 3 distinct primes.
102 is an admirable number.
It is a Harshad number since it is a multiple of its sum of digits (3).
It is a super Niven number, because it is divisible the sum of any subset of its (nonzero) digits.
102 is an idoneal number.
It is an Ulam number.
102 is an undulating number in base 4.
102 is a nontrivial repdigit in base 16.
It is a plaindrome in base 8, base 9, base 13, base 15 and base 16.
It is a nialpdrome in base 11, base 12, base 14 and base 16.
It is a zygodrome in base 16.
It is a congruent number.
In principle, a polygon with 102 sides can be constructed with ruler and compass.
It is a polite number, since it can be written in 3 ways as a sum of consecutive naturals, for example, 3 + ... + 14.
It is an arithmetic number, because the mean of its divisors is an integer number (27).
102 is a primitive abundant number, since it is smaller than the sum of its proper divisors, none of which is abundant.
It is a pseudoperfect number, because it is the sum of a subset of its proper divisors.
It is a Zumkeller number, because its divisors can be partitioned in two sets with the same sum (108).
102 is a wasteful number, since it uses less digits than its factorization.
102 is an evil number, because the sum of its binary digits is even.
The sum of its prime factors is 22.
The product of its (nonzero) digits is 2, while the sum is 3.
The square root of 102 is about 10.0995049384. The cubic root of 102 is about 4.6723287284.
Adding to 102 its reverse (201), we get a palindrome (303).
Subtracting 102 from its reverse (201), we obtain a palindrome (99).
Multiplying 102 by its reverse (201), we get a palindrome (20502).
The spelling of 102 in words is "one hundred two", and thus it is an aban number and an iban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.076 sec. • engine limits •

